論理回路と真理値表、なぜANDが論理積でORが論理和なのかについても わかりやすく【高校 情報Ⅰ、共通テスト向け】

例えば、
「ログインしてて かつ 新着のタブが押された場合、
　　会員専用の新着情報を表示する」

という処理を行わせるプログラムを書いたときなど。

「～場合」まで の 条件文。真か偽かが決まる文で、「かつ」,「または」でつながることもあるもの ーそれが論理式です。
「命題」とか「命題関数」とも 呼ばれるものです。

こうした論理式の演算処理が可能となるのは、コンピュータの内部がそもそも、論理演算を実現する 多くの細かい電気・電子回路でできているからなのです。
それら多くの回路１つ１つを、論理回路 と言います。

コンピュータはもともと「電子計算機」とも呼ばれるように、数値計算できる機能が根底にあって、論理演算はむしろ副次的な機能であるように思われるでしょう。

ところが実は、この論理演算の機能のほうが根底にあって、それら機能を組み合わせることにより、数値計算が、実現されています。

数値計算の 土台が 論理演算。

その土台を実現する、論理回路というものこそ が、まさにコンピュータの基盤とも言えるのです。
見ていくことにしましょう。

「回路」とは、そもそも何か？

「回路」とは「回るみち」と書き、英語でも circuit と呼ばれるように、電流が流れて１周するもの 全体 というのが、本来の意味でした。
電池に豆電球を１個つなぐような。

しかし回路が、多くの素子につなげて大きくなり、また集積化されたり、交流電源を採ったり高周波の信号を扱ったりするにしたがって、回路は、そのうちの部分部分に、分割して考えた方がよくなってきます。

分割した各部分のカタマリ。
そこに向かって 入ってくる( 入力 )電流や信号と、そこから出ていくもの( 出力 ) との関係に、注目するようになってくるのです。
もとの回路のうち、(まとまった機能を持つ) そうしたカタマリの部分のことも、「回路」と呼ぶようになりました。

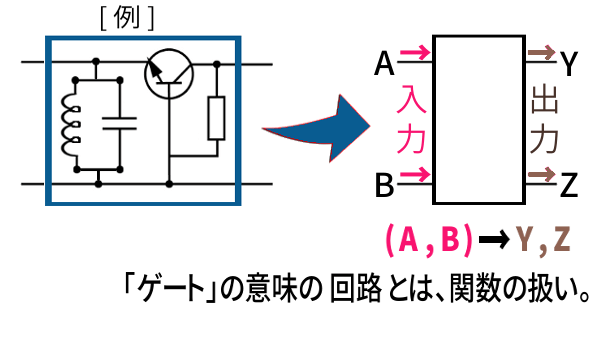
入力側の端子が２つのことが多いので、英語ではむしろ「ゲート」と呼ばれることが多いです。
入力側の端子 A , B からは、変化する電圧や電流による、電気信号 が入ってきます。
入力側の値に対する、出力側から出てくる信号の値が何かを把握すること。それが、関数として扱う 考え方。
「ゲート」の意味の回路は、関数として考えられます。

電気信号－ 音声やそれを変換した、波のようなもの。
いろいろな波の形を、そのまま扱うのがアナログ回路。
波形を 電流が流れるか否かの「０」,「１」によって近似して扱うのが、コンピュータのデジタル回路。
(「アナログ」/「デジタル」→ 「デジタル情報の特徴」)

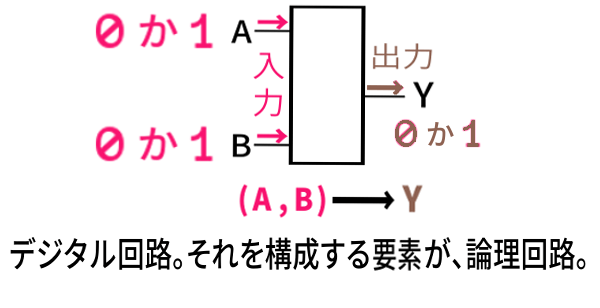
コンピュータのデジタル回路において、信号は
「０」か「１」かの２通り。だから コンピュータは２進法なのです。

まとめると、論理回路は、
・(「ゲート」の意味の )回路なので 関数として考える、
　つまり、入力と出力の値の対応を 把握すべき。　
・入力と出力の値が すべて「０」か「１」である
　デジタル回路の、基礎を構成するもの

ーなのです。

「０」,「１」による入力値と出力値の、対応を把握する方法が、この後で見る、真理値表を書いておくということです。

論理回路と その見かた

「０」と「１」の２種類のみが、論理回路に出入りする値の種類。
そして論理回路によって、論理式 ( 命題関数 )にかかわる処理を、実現することができます。
論理式は命題のことなので、「真か偽か」が大事です。
コンピュータは実は論理回路に基づき、「真か偽か」を「０か１か」で処理しているのです。

２通りの値しかとらない ことを、真理値 ( または、真偽値，ブーリアン ) といいます。
２通りの値ならば、「０か１か」でも「真か偽か」でも、構わないのです。

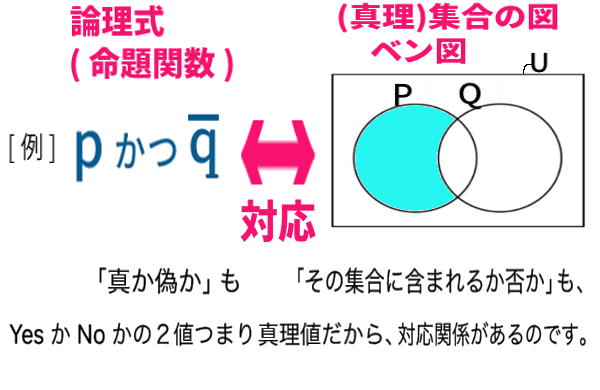
論理式 ( 命題関数 )はまた、集合と密接な関係があり、
(真理)集合を図示した ベン図 によっても、表すことができました。

そこで注意すべきなのは、

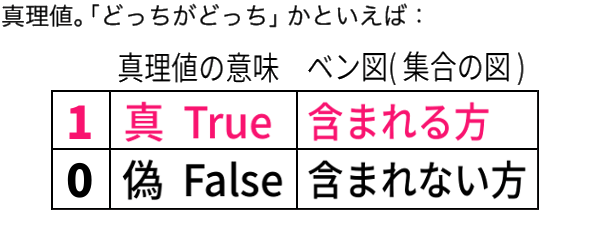
なぜ、真が「１」のほうであり、逆のほう「０」ではないのか？
「条件を満たす」方が「ある」方で、「満たさない」方は「ない」方。そう考えた方が しっくりくるからだと思われます。
例えば色の３要素など、その原色の「含まれる」方が「ある」方で、「ない」方はゼロと考える方が便利です。

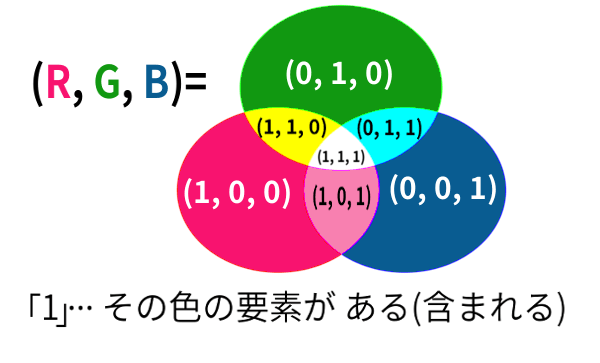
「1」が「真」であり「含まれる」の方
なのです。

このことを確認した上で、いよいよ、具体的な論理回路を見ていくことにしましょう。

論理回路と真理値表

まずは AND回路( 論理積回路 ) から見ていきます。
回路には、その挙動を把握する仕様書として、表が添付されています。
入力端子それぞれから、入力値「０」か「１」が入ってくる、その あらゆる 場合の、各々に対応する出力値を、一覧にまとめたもの。真理値表というものです：

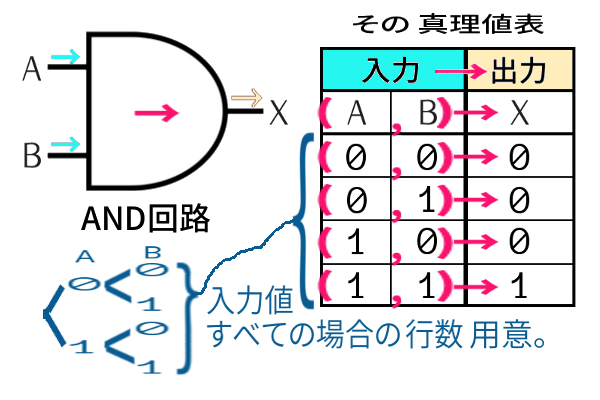
真理値表が完全なものであるために必要なのは、
入力値のあり得るすべての場合＝２の 入力端子数乗 ぶんだけ、行数を用意しなければならない ことです。
AND回路については、入力端子は２つなので、２ビット分の情報。樹形図を描いても理解できるように、情報のすべての場合は ２の２乗つまり４通り。
だからその真理値表は４行必要というわけです。

入力値のパターンを各行、列挙するには、０→１の順。
２進法で数を数える順番に挙げていくのが推奨です。
もれのないよう分かりやすく挙げねばなりません。

真理値表の形式についての注意は以上ですが、
「０」や「１」が書いてある 真理値表の 意味( 内容 )は一体？。
今はAND回路。その出力値を判断するための、真理値表の読み方です：

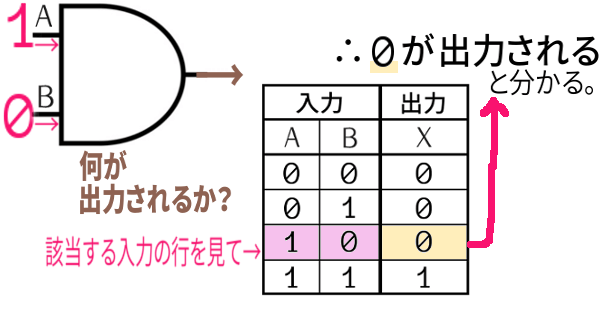
そのときの、各入力端子からの入力値のパターンに該当する行を見ることによって、何の値が出力されるか、分かるようになっているのが、真理値表なのです。
実際の回路にそのような入力値を入れると、その出力値が出てくることを表しています。