1次連立不定方程式(合同方程式) [余りの整数問題] を解く 軌道(orbit)解法 ～中国式剰余定理

例えば次の問題が、古代中国の文献に出ています。
数値も同じまま よく引用され、非常に有名なものです:

中国式剰余定理という …

ことを主張する定理があります。

この中国式剰余定理 はもちろん高校の範囲外ですが、それを知っていれば、問題を解くために役に立つのではないか？ と期待されます。
しかしそれは叶いません。
あくまでも、そのような余りの値が「一意的に存在する」という存在・分布定理なのです。
冒頭のような問題が、余りの値を任意にとったとしても、問題として成立することを保証するもので、その時代の中国では既に、そうした余りの性質が知られていたと推察されています。

上記定理は触れるだけしましたが、やはり実際に答えを得るためには、オーソドックスに、１次不定方程式を解くことが原則。
しかも余りの条件が3つ以上なので、１次連立不定方程式となるでしょう。そこで、

1次連立不定方程式による解法

を紹介しておきます。
「 3で割った余りが 2、5で割った余りが 3、7で割った余りが 2 」なので

そのうち、3で割った余り と 7で割った余りが 2 でそろっているので、第 1 辺と第 3 辺はまとめられ、最小公倍数 21 で割った余りが 2 であるといえます。
だから１個の不定方程式となるので、それを解きます:

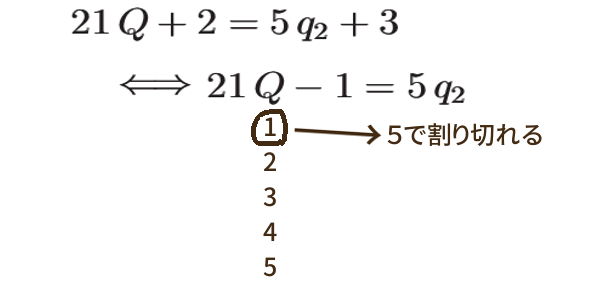
21 と 5 も互いに素なので、21にかけられた Q は連続した 5 整数の中で１通りだけ、条件を満たすものが見つかります。
したがって、\( (\,Q\,,\,q_2 \,) = (\,1\,,\,4\,) \) が得られ、もとの左辺および右辺の値 23 が、求める値となります。
求める値が 0 以上 LCM( 3, 5, 7 )＝105 未満の中でただ１通りであることは、先の 中国式剰余定理 によって保証されています。

問題の中に、もしそろっている余りの値がない場合、解き方の後半のような1次不定方程式を、２度解かねばならないでしょう。
もっとうまいやり方はないものか？ … そこで、商・余りの性質を活かした次の解法を紹介します。

軌道(orbit)解法によれば…

問題を再掲すると、

これを以下のように解答します:

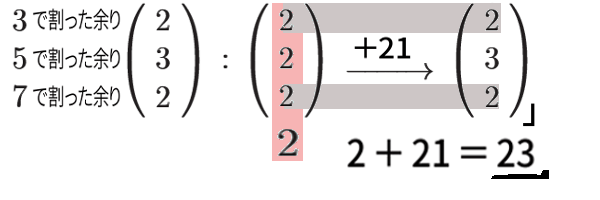
多くの余りの値が 2 でそろっていますので、数値 2 からスタート。
2 は 3 , 5 , 7 のいずれよりも小さい数なので、いずれで割った余りもすべて 2 となり、2 , 2 , 2 と書けます。
各 余りを 縦に書いておきましょう。
それに、最小公倍数 3×7＝21 だけ足せば、3 , 7で割った余りは動かないようにでき、5 で割った余りは 21÷5 = 4 余り 1 だから 1 だけ足された値になるから、2 → 3 と変化します。
これで問題の 各余りの値 に一致しましたので、答えが得られました。

各余りの値がそろってない場合はどうするでしょうか？。
より複雑な問題に改題してみると:

今度はそろってる余りの値はないので、とりあえず 3 で割った余り 2 に合わせてスタート:

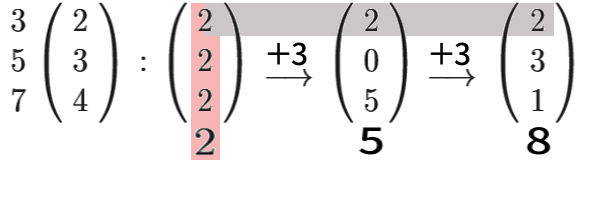
実際の数( 105 で割った余り )を、下に書き添え、3 で割った余りだけが動かない 3 ずつ、増やしていきます。
増やす操作を 2回行ったところで、5 で割った余りも合いました。
3 と 5 で割った余りまでが合ったので、これら２つの数の余りが動かないよう、3 と 5 の最小公倍数15 ずつ移動させましょう:

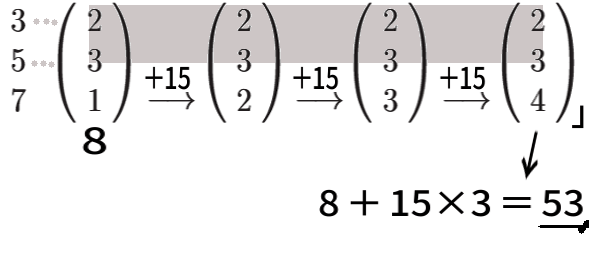
15 ずつ足せば、7 で割った余りは 15÷7 = 2 余り 1 だから 1 ずつ足されていきます。
だから、15 を 3 回足したところで、7 の余りも合わせられました。

もし 15 を何回も足していき、105 を超えてしまうことがあっても大丈夫です。
105 を引いて、あくまでも 105 未満の数にすればよいだけだからです。
存在と一意性についてはやはり、冒頭に掲げた、中国式剰余定理によって保証されています。