二分探索のアルゴリズムを、コードなしでわかりやすく解説。その最大探索回数が [ log_2 n ]+1 である証明も【高校 情報1 探索のプログラム】

高校情報1 では、「探索のプログラミング」として、主に2種類(線形探索と二分探索)を学習します。
そのうち、二分探索 ( binary search ) とは
データの中から、特定の値(数値や文字列)を探索するためのアルゴリズム (その問題を解決するための、コンピュータでのプログラミングの手順) の一つ。
半分個ずつに分割を繰り返すことによって しぼり込んでいく方法です。
データの個数 n が大きくなっても、非常に早く探索できる有効なアルゴリズムです。
ただし「二分探索」の「二分」は 「にぶ」ではなく「にぶん」と読みます。
以下で詳しくみていきましょう。
二分探索とは~ソースコードなしで

半分個ずつに分割して「63」の含まれる方を採れば
{ 42, 50, 63, 70 }。これが1回目の操作。
次また、半分個ずつにして「63」を含む方を採り
{ 63, 70 }。これが2回目の操作。
次また半分個ずつで63、1個だけに到達、3回目の操作。
8個→4個→2個→1個となり特定完了。
「半分個ずつに分割して探索する値を含む側を採る ことの繰り返し」が、アルゴリズムの概要です。

2の累乗の指数、\(k\)回で探索完了。確かに今の例、
\(n=8\) では3回で完了していますね。
この例の データ数くらいでは あまり早さ( 回数の少なさ )は実感できませんが、
それがもし データ数\(n=1024(\,=2^{\,10}\,)\) 個であったら、たったの \(k=10\)回目にして1個にしぼられるということ。
データの個数が多いほどその早さが分かるでしょう。
実際には \(k=3\)回とか 10回のような、個数2の累乗の 指数の値そのもの だけが探索回数とは限りません。
実際の方法では、データの中央値のときは1回で探索完了 ということさえ あるのです。
またデータ数も、8とか64, 128とか1024のような2の累乗 個 とは限りません。
先ほどの概要はあくまで見易い例でしたが これから、
実際のアルゴリズムを見ていきましょう。
そのとき、データの方にも実は 前提 があって、採ってきてそのままのデータに、すぐアルゴリズムを適用できるかというと そうではないのです。
その点から確認していきましょう。
まず探索をかけるべきデータは、予め整列されてあること
「整列」とは、値の小さい順 (「昇順」) または大きい順 (「降順」) や、文字列であれば「辞書式順序」など、
一定の順序に従って並べておくことです。
要素の重複も、何らかの形で取り除いておきます。
そのようにあらかじめ整えておかないと、二分探索はうまく行えません。
先ほどの例では、
{ 12, 21, 29, 38, 42, 50, 63, 70 } のうちから「63」を探そうと、
{ 12, 21, 29, 38 } と { 42, 50, 63, 70 } とに二分して、「63」を含む方に しぼっていきましたが、
もしデータが
{ 12, 63, 42, 50, 29, 21, 70, 38 } のような でたらめな順序だと、
{ 12, 63, 42, 50 } と { 29, 21, 70, 38 } とに二分してみて
「63」を含む方に しぼりたくても、
どちらが「63」を含むのかは、結局全部調べない限り、
すぐには判定できず、二分する意味がなくなります。
だから二分探索を適用する前提として、データは予め整列させておくことです。
ここではデータは昇順(小さい順) に並んでいるものと仮定していきましょう。
ついでに、データのような複数の値は、多くのプログラム言語では「配列」とか「リスト」といった
しくみ ( 変数型 ) を構成し、記憶したり利用します。
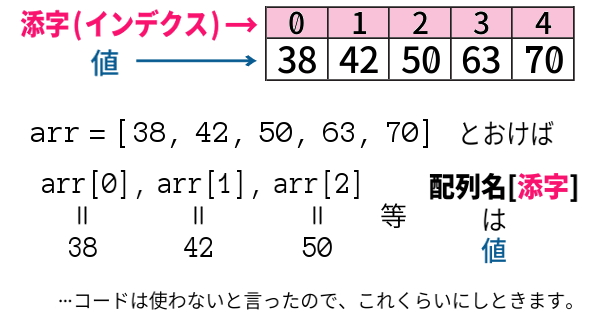
列挙した値を格納するときに、添字(インデクス) を振っておくのが、配列というしくみ(「型」) なのです。
数列 ( \(a_1 ,\, a_2 ,\,\dotsm\) ) みたいですね。
ただしインデクスは、0番から 振り始めることが多いので注意しましょう。
ほとんどのプログラム言語ではそうです。
データが昇順に並び 配列に格納されたところで、いよいよアルゴリズムの適用です。
そして「半分個ずつ」に分割する
実際にはどうやるか。
真ん中で 分割しなければなりませんので、「中央の場所」を はっきりさせなければいけません。
そのためには、添字(インデクス) を使って計算します。
左端のインデクスを L、右端のを R として、
たして 2で割れば 求まります。
次の例はデータ数\(n=7\) 、
\((L+R)/2\) は \((0+6)/2 = 3\) と求まります。
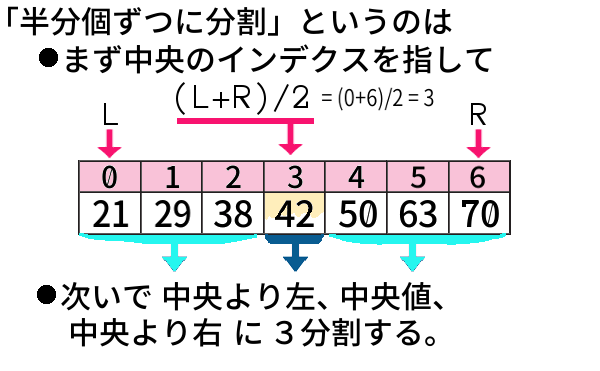
「二分」,「半分個ずつに分割」と言いましたが、
実際には3分割 なのです。2分割ではありません。
中央のインデクスの値 つまり 中央値に注目するついでに、中央値と探索する値が 等しいかどうかも、ここで判定してしまうのが、早いから(それ以外にも理由はあるのですが、後述します)です。
もし今のデータから「42」を探索するという場合、たった この1回で探索完了となります。
もしそれが「63」を探索する場合には、どうするでしょうか?
あわせて、探索する値を含む「側」に しぼり込む操作
これを行う必要があります。どうやって?
ー やはり、インデクスで指し示すことで、できます。
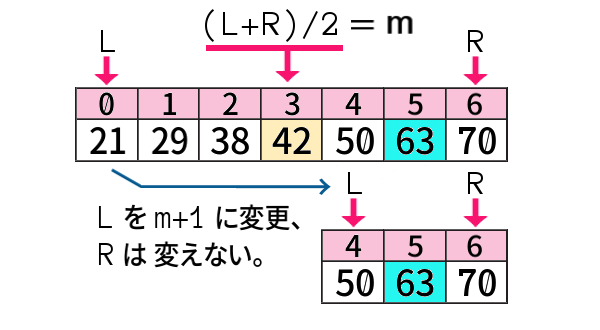
「63」は「中央より右」の配列、具体的には「インデクス4~6」に含まれるので、左端のインデクス L を、「0」の代わりに「4」へと変更してあげるのです。
そもそも「『中央より右』の配列の側に含まれる」と判断した 条件は 何か というと、
中央値だった「42」よりも、探索値「63」の方が大きいからです。
データは今、昇順に並んでいましたので、より大きい値ほど右にあるからです。
データが整列されていれば、中央値と探索値の大小 だけ を見ることで、探索値が中央値よりも 右側にあるか 左側にあるか を判断できます。
何百何千のデータ数であっても、そこだけで、判断することができるのです。
同様の考え方で、例えば「38」を探索したいとき。
条件設定から順序だてて述べれば、
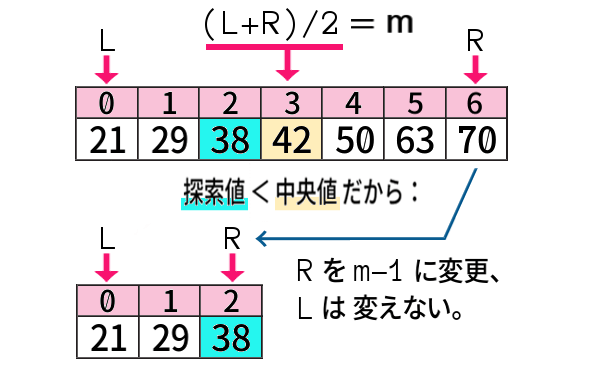
このようになります。
中央値に着目し、中央より左側と中央値と中央より右側とに分割して、探索値を含む側にしぼり込む
~ そこまでが、一連の操作 1回分。
この一連の操作を、何回も 繰り返す
その結果、しぼり込まれていった配列の要素の個数が1になったところで、じき探索は完了(「見つかった!」)していくわけです。
今のデータで、「38」を探索する様子と「63」を探索する様子を、同時に1枚に図示すれば、次のようです:
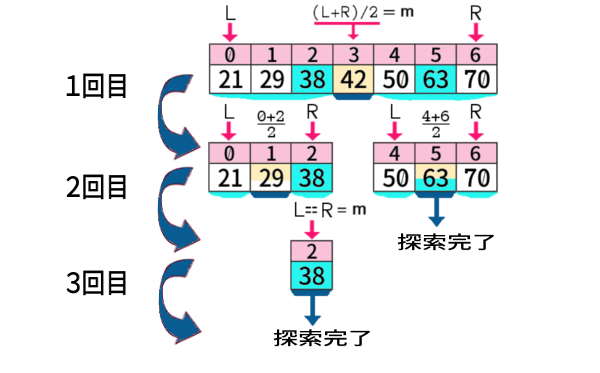
その回で探索する配列のうちの中央値が 探索値と等しい場合には、その回で探索は完了です。
また 中央値以外で、探索する配列が1個の要素だけになった場合は、その次の回で探索は完了です。
次の回で、配列のL\(=\)R なので、その中央のインデクスm とも等しいことになり、その要素自体が中央値となるからです。
「1個だけの要素になったら、探索完了は近い」と考えて正しいですが、必ずその回で完了するわけではなく、あくまでも完了する契機は、探索値が中央値に一致すること、それだけです。
前の方で、配列を分割した時 すぐ、中央値が探索値と一致するか判定してしまうのには、その方が早い以外の理由がある と言ったのですが、それが、探索を終わらせる 最も簡単な 契機(トリガ) だからです。
「1個だけの配列になった」ことを以て探索完了の契機にしようとすると、その条件の記述はやや煩雑になってしまうのです。
ただし実は 中央値というか「左中央値」。
以上の例では、データ数\(n=8,\,7\) と見てきましたが、要素をさらに1個落として、\(n=6\) にしてみましょう。
多いデータの個数でももちろん、少ない任意の個数でも、うまくできなければいけません。
まず、中央のインデクスm \(=(L+R)/2\) の計算から。
すると、
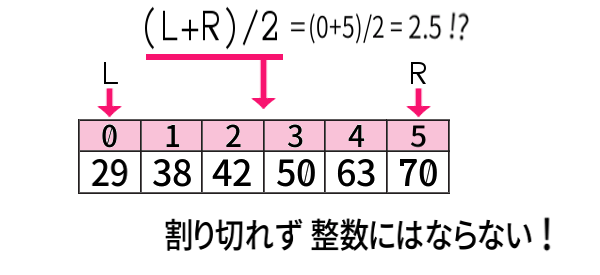
実は\(n=8\) でも、よく見れば、起こっていたことです。
こういう(偶数個の) ときは、次のように決めます:
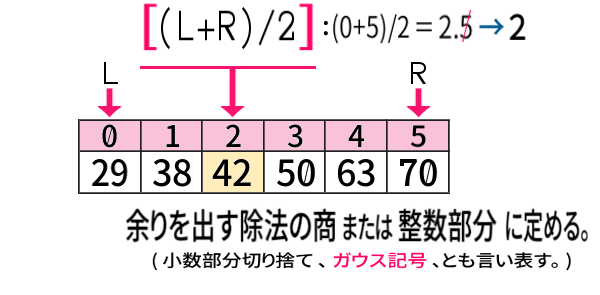
中央値というか、中央の値が2個ある場合には左の方の値に定めることになるので、「左中央値」と呼ぶべきものです。
両端のインデクスをたして2で割ったとき、割り切れなければ小数を切り捨てます。
「四捨五入」や「切り上げ」ではなくなぜ「切り捨て」かというと、割り切れる場合と分けずに、最も簡単に、プログラム言語に既存の演算子で計算できるからだと考えられます。
数式を少し使うと、中央のインデクスm を求めるためには以後、
割り切れても割り切れなくてもm \(=\)[ \((L+R)/2\) ] 。
数学で出てくるガウス記号。例えば [ 3 ]=3, [ 3.5 ]=3 です。憶えておくとよいでしょう。
(ただし、負の数ではガウス記号の値が整数部分を表さないことは一応、注意です。)
「半分個ずつに分割」と、前半では便宜上説明しましたが、実は語弊があって、正確には「左中央値の前後で分割」です。
あくまでも「左中央値」であって、「情報1」の教科内の他分野や 中学・高校 数学1の「データの分析」などで出てくる「中央値(メジアン) 」とは異なります。
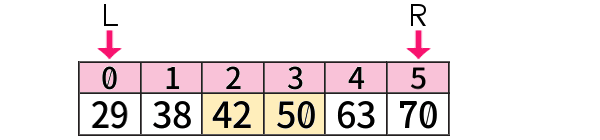
中央値(メジアン) は、いわば中央の値が2個ある場合は それらをたして2で割る、
今の例でそれをやるならば、(42+50) / 2 = 46 と求めるでしょう。
割り切れなければ、小数のまま出します。
ところが統計処理とは異なり、今やっていたことは、探索 でした。
この算出した「46」はもともと、探索データにはなかった値。
それを相手にしてみても、もともとあった値の中から探し出すという今の目的にとって、意味はありません。
探索のアルゴリズムで把握する 真ん中の値は、統計の「中央値(メジアン)」ではないのです。
今のデータ(\(n=6\))で「38」を探索する様子と「63」を探索する様子を、同時に1枚に図示すれば、次のようになります:
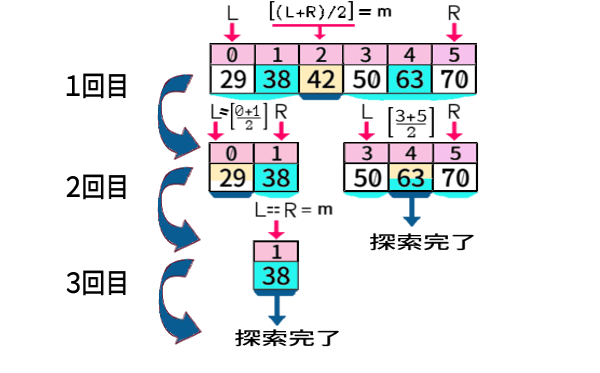
要素数\(n=2\) の配列の場合、L\(=0\) , R\(=1\) で、
左中央のインデクスm\(=\)[ (L+R)/2 ] は、[ 1/2 ]\(=0\) 。
左側の値がまさに 左中央値になっています。
以上、二分探索のアルゴリズムの流れを、平文でまとめると:
- 「左中央」のインデクスm\(=\) [ (L+R)/ 2 ] の値(「左中央値」)に注目。
- それより左側と「左中央値」と それより右側 に、配列を3分割。
- 2.で、探索値が「左中央値」に一致していれば、探索完了。
- 3.以外ならば、探索値を含む側( 不等号で評価 ) の配列に しぼり込む。
- 探索完了でない限り、1.に戻って繰り返し 次の回目へ。
この繰り返しの回数を数えたものが、探索回数です。
二分探索の探索回数
これまでいくつかの例で、「38」や「63」が探索される様子を見てきました。
ここではさらに、データ数を決めたときの、
中にある 任意の(インデクス番め にある) 要素それぞれの 探索回数を 見てみましょう。
すべての要素を相手にするのです。
手始めに、少ないデータ数\(n=1,\,2\) の場合から。
例として「29」や「38」としていますが、各値は、昇順であればどんなでも構いません。
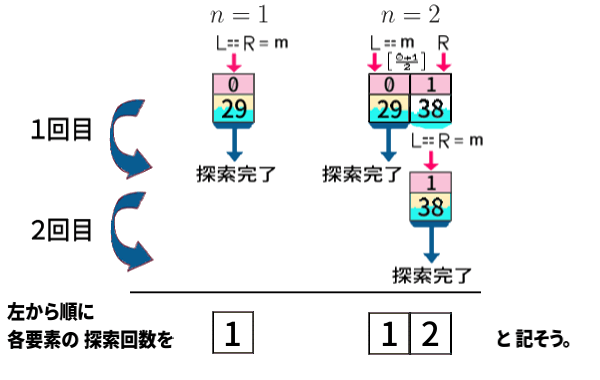
このように、探索回数を列挙して表しましょう。
\(n=2\) で「左中央値」は0番め つまり 左側の値の方でしたので、0番めの方が早く1回で探索完了となるわけです。
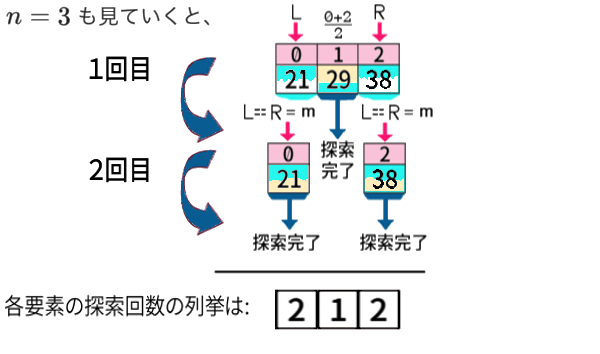
次は少し飛んで、\(n=6\) を見てみましょう。
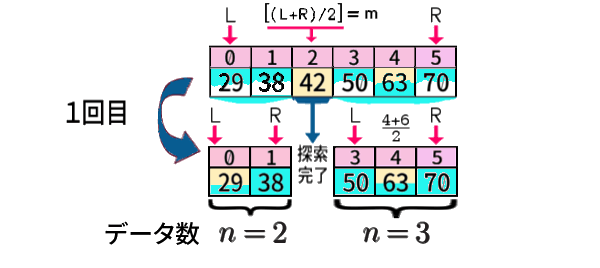
1回目まで行いました。しかし2回, 3回 … と行わなくても もう分かるのです。
インデクス2番めの「左中央値」は、まず探索回数1です。
その前後の配列のデータ数(要素数) は、それぞれ2個, 3個 で、実は先ほど調べた、\(n=2,\,3\) の場合。だから、
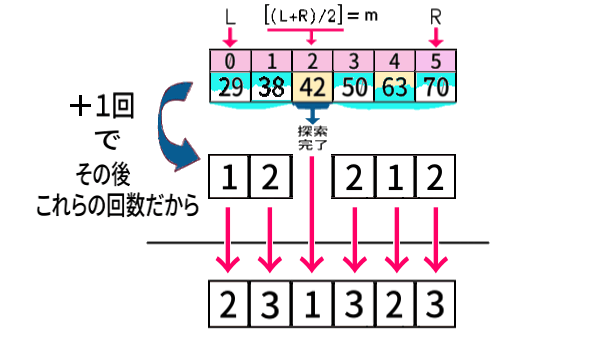
のように、探索回数の全列挙は、求めることができます。
より少ない\(n\) のとき求めた結果が使える (再利用) ことを、再帰的と言います。
二分探索のアルゴリズムは、再帰的プログラミングも可能なのです。
これら探索回数の列挙を、
探索回数表にまとめてみる
ことをやってみます。「左中央値」だけは1回で探索完了する、いわば最小値なので、「1」で揃えて見てみます。
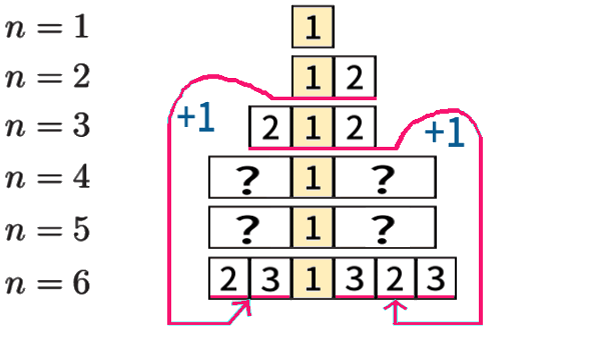
\(n=6\) の場合は、\(n=2,\,3\) の場合(を+1 すること) を再利用して求められるのでした。
\(n=4,\,5\) の場合はまだ求めていませんが、やはり再利用を使えば簡単です。
そもそも、\(n\leqq 3\) の場合でさえも、
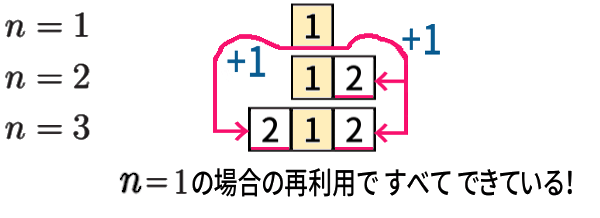
ー と言えるのです。
\(n=4,\,5\)の場合も含め、6までをすべて求めれば、
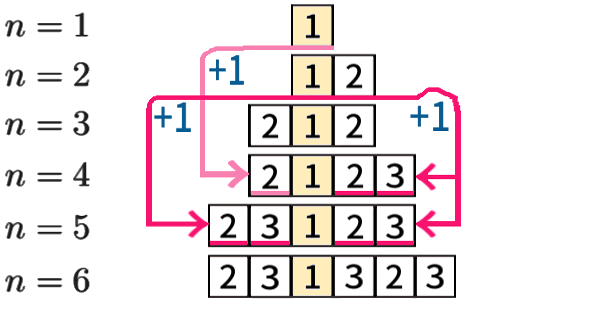
\(n=3\) までの再利用で できていることが分かります。
「\(n=3\) まで で生成される」とも言います。
囲みの四角を取っ払って、もう少し出してみましょう。

線で区切った理由の1つは、最大探索回数の大きさ (1, 2, 3, 4, … となって行っている) によって です。
データを左中央値の所で3分割するとき、
そのデータ(総)数=
左側の配列の個数+左中央の個数(=1)+右側の個数 で、
右側の個数ー左側の個数=0 または 1
ですので、青丸のように計算できます。
1, 3, 7, … とは \(2^k -1\ \ (k\text{は自然数})\) と分かるので、

と言えます。
これが、次のことの証明を可能にするのです。
データ数 \(n\) のとき、最大探索回数が \([\,\log_2 \,n\,]+1\) であることの証明
上で分かったことをもとにして、証明には数学的帰納法を使用します。

