デジタル情報の特徴とその単位、10進法と2進法と16進法の変換計算(整数)をわかりやすく【高校 情報Ⅰ、共通テスト向け】

高校教科 情報Ⅰでは、PCやスマホ・タブレットなど
コンピュータ が どうやって計算しているか、そのしくみ について、学習していきます。
デジタル情報とアナログ情報
0と1の 2種類の数字を並べていってできる信号が
デジタル情報 と呼ばれるもので、コンピュータが扱う情報の形式です。
コンピュータ内部は細かい電気・電子回路になっていて、通電する/しない をもとに 演算がなされるからです。
対して、実世界で見えるもの(画像や映像) や音声などは
アナログ情報 と呼ばれるもので、コンピュータで扱うためには、デジタル情報に近似・変換される必要があります。

離散量とは、とびとびの値をとる量のことです。
0, 1 だけで終わらず、例えば 2, 3, 4, \(\dotsm\) という値もあり、しかし2.5とか3.333のような 間の値は とらない、といったときも、離散量です。
デジタル情報とはとくに、1つの情報単位あたり 0と1の2通りの値しかとらない離散量です。
数字が 0と1の2種類しかない世界なのです。
そこで、
0と1の2種類の数字 だけ で数えてみる:
0, 1 その次。「2」やその先の数字はありません。
どうすればよいでしょう?。
【ヒント】。いつもの 数の数え方では、
0, 1, 2, 3, 4, 5, 6, 7, 8, 9 まで 言ったら 次は 10 です。
数字を すべて言ってしまった後、
桁(けた) が くり上がって 下の桁は0にしますね。
0, 1 その次は だから、10 となります。ただし
「じゅう」と読まずに「いちゼロ」と読みましょう。
0, 1, 10, 11(「いちいち」)、その次は?。
1を足していく と考えてもよく、
一番下の位が くり上がり 上の位に1が足され、すると
また くり上がらなければならない! だから…
100 となります。これも「いちゼロゼロ」と読みましょう。
0, 1, 10, 11, 100, 101, 110, 111, (慣れてきて)その次も
全ての位が1だから くり上がり、1000 となります。
このような数の数え方を、2進法 と呼びます。
2進法では数字が0と1の2種類しかないから、どんどんくり上がっていきますね。
いつもの数の数え方は 10進法 と呼びます。これの読みは「じゅっしんほう」です。また10進法で表した数 10 は「じゅう」であり「いちゼロ」とは読みません。
10進法と2進法による 数え方、比べてみると こうなります:
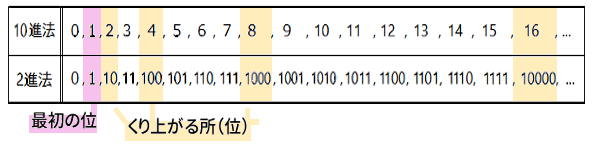
最初の位 から始めて、くり上がる所(くらい) だけ見ていくと、
\(\ 1\,,\,2\,,\,4\,,\,8\,,\,16\,,\dotsm\)
2倍、2倍になっていってる!と分かる つまり、
2をどんどん かけていく、2の累乗 だと分かります。
\(\ 2=2^1 \ ,\ 4=2^2 \ ,\ 8=2^3 \ ,\ 16=2^4 \ ,\dotsm \)
「0乗」も 定義できて、値は1(理由は後述)。
\( 2^0 =1 \) ということで
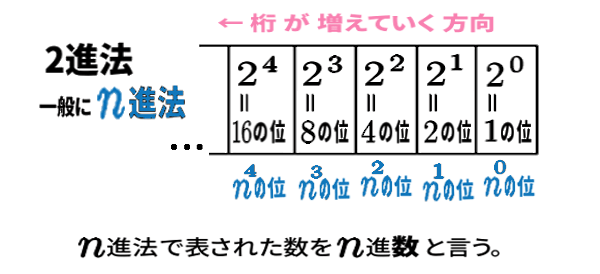
\(n\)進法で 各桁は、末尾の位(右) から順に
\( n^{\,0}\,(=1)\text{の位}\,,\, n^{\,1}\,(=n)\text{の位}\,,\, n^2\text{の位}\,,\dotsm\)
確かに10進数でも、\( \text{壱の位}\,,\, \text{十の位}\,,\, 10^2=\text{百の位}\,,\dotsm\)
となっていますね。
でもなぜ、位は累乗になるのか? 疑問があるかもしれません。
それは少し後で、詳しく見ていくことにします。
1の位、2の位、4の位、\(\dotsm\) そういう
2進法の 一つひとつの 桁(位) のことを、
ビット bit と とくに、呼びます。
” bit ” と言っても「かけら」の意味の方でなく、
「binary digit」の略語です 実は。
そうそう 数えるとき大事な点1つ確認しておきましょう:
コンピュータでは、1番ではなく 0番から数え始める!
ビット数 と 表現できる状態の数:「状態数」
「表現できる状態の個数 (状態数)」とはつまり、
そのビット数(桁数) で いくつまで数えられますか?
相異なる数は 何通りできますか?
ーという意味です。例えば 3ビットの場合、
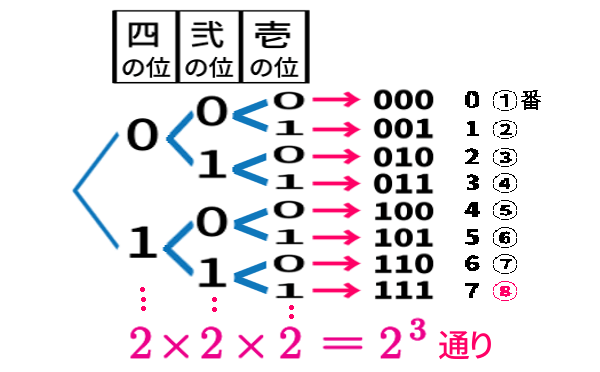
樹形図です。
各ビットについて0か1かの2通りに枝分かれ。
その次のビットで また2通りに枝分かれ… だから
かける2…
3ビットだと、2を3回かける のだから 2の3乗つまり8通り。
それが、3ビットで数えることのできる個数。
①番から数え始めれば8まで。0から数え始めるから1つ手前の7までですが。
一方8とは、3ビットすべてが1になった次の、4ビットめに初めてくり上がる数( 1000 )。
3ビットで数えることのできる個数とは、4ビットめに初めてくり上がる数でもあるということなのです。
一般に \(s\)ビットであろうと、\(n\)進法の\(s\)けた であろうと、同様のことが言えます。まとめると:

これで、「位が 累乗になる」ことの真の理由も説明できました。
例えば10進法でも確かに、一桁に使える数字が、0から9までの10通り。だから10進法と言い、
だから、例えば10進法で3桁だったら、000 から 999 までの1000通り\( =10^{\,3}\) ということで、上の原則通りであることが確認できますね。
2進法に話をもどして、10ビットまでの状態数 の値は よく出ます。憶えてしまいましょう:

\(\ 2^{\,11}\,\)以上はあまり憶えなくてよいです。必要なときは、2をかけていく計算をして出します。
しかし \(\ 2^{\,16}=65536\,\) だけは、憶えておくようにしましょう。16ビットの状態数です。
累乗というものは増大のしかたが激しい特徴があり、
手計算は大変になっていきます。
もし、16乗を超える2の累乗が出たら、
指数までは 計算しておき、
累乗の形のままで答として構いません。
また、次でみていきますが、ビット数8個つまり8ビットぶんで、1バイトと呼ばれます。
そしてビット数やバイト数のことは「情報量」と言い、「状態数」とは区別します。
状態数の計算と 情報量の単位
今もふれましたが、まず、
バイト Byte という単位があります。8ビット で 1バイト です。
それなら、2バイトは何ビットでしょうか?
そうですね。\(2\times 8=16\,\)ビット。かける8 すれば出ます。
次。2バイトで表現できる状態の個数 (状態数) は、いくら(いくつ)でしょうか?
そうですね。2バイト\(=2\times 8=16\) ビットだから、\(2^{\,16}=65536\,\)と答えられます。
そういうきき方の問題もよく出ます。
状態数が問われたら、
情報量のバイト数は まずビットに変換するようにし、
その上で、2の累乗です。
大きい数になりそうならば、累乗の形のまま計算したり、答えて構いません。
そこで、累乗の計算に強くなりましょう。復習すべきは:
累乗の基本性質 とくに「指数法則」

状態数を計算するとき、2の累乗ですから、
底 (テイ) が2、と言えます。
右側の2式が、累乗の基本性質【指数法則】。
まずは 1, 2, … という 正の整数( 自然数 ) を指数とした \(p,\,q\) について成り立っています。
( 底 \(a\) は2など正の数でなければなりません。 )
詳しくは 数学Ⅱで学習し、情報科の計算でも使います。
この指数法則をもとにすれば、自然数よりもっと広く、0や負も含んだ 整数一般の指数が、意味をもつと分かるのです。
「指数の拡張」と言います。以下復習しましょう。
指数法則の利用でまず、「0乗が1」になる理由が分かります。実際、
\(a^{\,p}\,\times\,a^0 = a^{\,p+0}=a^{\,p}\) ですから、
\(a^{\,p}(\neq 0)\) に \(a^0\)という値をかけても \(a^{\,p}\) のまま変わらない。
すなわち、\(a^0\) の値は1でなければならない、というわけです。
「0乗が1」が分かったら次は、負の数の指数が考えられるようになります。実際、
\(a^{\,p}\,\times\,a^{-p} = a^{\,p-p}=a^0\) という計算を考えて、
\(a^{\,p}\) に \(a^{-p}\) という値をかけたら、1になるわけだから、
\(a^{-p}\) という値は、\(\dfrac{\,1\,}{a^{\,p}}\) つまり 逆数であればよい ということですね。
「負の指数は逆数」ということが分かりました。
自然科学で出てきますが、例えば \(10^{-3}=\dfrac{1}{10^3}=\dfrac{1}{1000}=0.001\) ということです。
すると、指数の引き算を考えることができます。
中学の時は覚えさせられたと思いますが、高校では、指数の足し算の指数法則だけから、導くことができるのです。実際、
\( a^{\,p-q}=a^{\,p}\times a^{-q}=a^{\,p}\times\dfrac{1}{a^{\,q}}=\dfrac{a^{\,p}}{a^{\,q}}\)
「指数の引き算は割り算」ということが分かりました。
しかし指数の引き算。逆さに引くと 間違うので、確認を書いておきます:
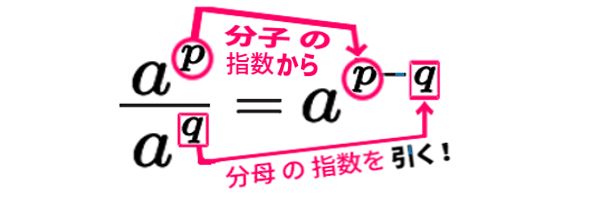
演習として、次の【例題】を 解いてみましょう:
(1) 3バイトで表現できる状態数は 2.5バイトの 何倍か、
(2) 教育漢字 1026 字を表現するためには、何ビット必要か?
【解】
(1) 3バイトは、3 × 8=24ビット。
2.5バイトは、2.5 × 8=20ビット。
状態数で比べると、\( \dfrac{2^{\,24}}{2^{\,20}} =2^{\,24-20}=2^{\,4}=\)16 倍。
(2) (状態数)=1026 は、\(2^{\,10}=1024\,<\,1026\,\leqq\,2^{\,11}\)
だから、11ビット必要。
「表現する」「表現できる」とは、識別できる
という意味です。
例えば教育漢字ですので、「海」という字を32番、
「山」という字を35番に割り当てる、というふうに、
全1026字に、相異なる番号を割り当てられれば
十分である、という意味です。
「海」なら「海」という字を、具体的に黒と白の
ドットで表現しようとすればそれは、
11ビットでは到底足りませんが、
そういう意味ではないのです。
それに、
なぜ 1バイト=8ビット という単位が大事なのか
というと、「8」という数が、また2の累乗で表される数だから、というのが1つの大きな理由です。
実際、8ビットコンピュータ、16ビットコンピュータ、\(\dotsm\) というように、コンピュータは進化してきています。
情報量の もっと大きな単位
情報量 ~ビット数やバイト数~ には、さらに大きな単位がありますが、注意点があります。
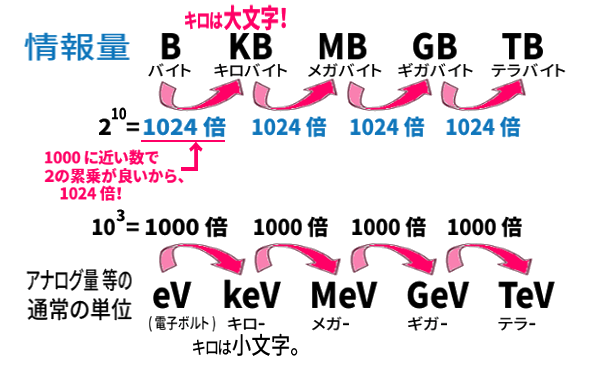
まず、アナログ量など 通常の単位にある、
キロ、メガ、\(\dotsm\) は1000倍ずつですが、
デジタルの情報量の場合、キロ、メガ、\(\dotsm\) は1024倍です。
1000に近くて2進法になじむ数値が採用されたためだと言われています。
また、情報量の「キロ」は、通常の単位の「キロ」と異なり大文字で表されることが多いです。
米国のIT大企業が始めた慣用ですが、単位を管理する国際機関の同意は得られていない現状です。
ちなみに、テラ の次は何かというと、P( ペタ )、E( エクサ )、\(\dotsm\) と続きます。
やはり 情報量については1024倍ずつ、通常の単位では1000倍ずつになります。
これまでの、状態数と情報量についてまとめると:
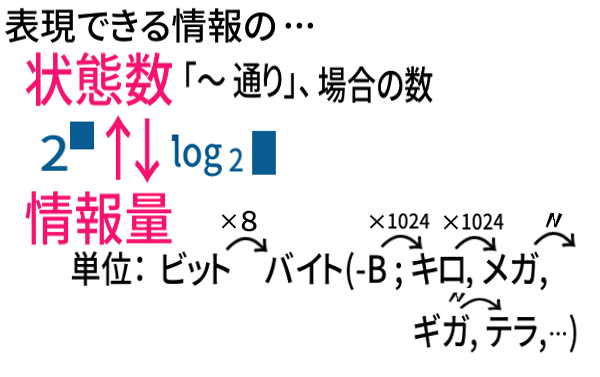
16進法(十六進法)
今度は2進法でも10進法でもなく、16進法 です。
16進数 もまた、コンピュータが扱いやすい 数の表し方なので、数え方に慣れていきましょう。
0,1,2,3,4,5,6,7,8,9まで数えたら 次は、「10」ではありません。
10進法でいう16(十六)になるまで、次の桁にくり上がってはいけないのです。
ひと桁の中だけで数えなければならない。
すると10進法の数字は0から9までの十種類だけだから、数字が足りません。
そこで、A, B, C,\(\dotsm\ \)も数字として使用!
数字は何種類 必要か? 10進法で数字が十種類だから、16進法ならば十六種類 必要。よって、
0,1,2,3,4,5,6,7,8,9, A , B , C , D , E , F までが要る、というわけです。
そこまで数えて、初めて次の数が 10 です。10進法以外なのでこれも「いちゼロ」と呼びます。
同様に、
10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F, 20,\(\dotsm\)
と続けていきます。
そのように数え続けていったとき、もう少し後の数のことを考えてみましょう。
3桁目にくり上がる直前の数は、いくつでしょうか?
そうですね。最後(最大)の数字が F なので、2桁とも F 。FF です。
そうしたら、FF とは 10進数の いくらでしょうか?。
先ほどやったことを思い出しましょう。
\(n\)進法の \((s+1)\)番目の桁は、\(n^{\,s}\) の位 でした。
直接の計算方法は この後に回して ここでは、次のように計算してみます。
FF の 次の数が初めて3桁めの出る数 100 なので、\(n=16\) で \(16^{\,3-1}=256\) (の位)。
FF は、その1つ手前の数なので、255 と分かります。
今度は なかなか くり上がらない数え方なので、たった2桁なのに、これほど大きな数なのです。
「16進法」は英語では “hexadecimal” です。
“hexa-” がギリシア語由来の「6」で、”decimal” は「10進法」という意味で ラテン語由来です。
余談ですが、語順からすると「60」はどうするのか、と疑問に思う人もいるでしょう。
「60進法」に相当する英単語は、”sexagesimal” と、ラテン語由来で表します。
(10進法での)1の位はギリシア語由来の接頭語で、10の位の部分はラテン語由来の語幹で表すのです。
「\(n\) 進法」の\(n\) が10未満の場合は、主にラテン語由来である英単語で表します。
例えば「8進法」は “octal” で、「2進法」は “binary” です。
さてこの後でいよいよ、いろいろな進法 の変換計算を考えていきます。
そこで遅くなったのですが、混乱しないための記号の注意です。
今後、10進法以外の \(n\)進数表示では、
右下に小さく “\((\,n\,)\)” と記すようにします。
例えば、\(1010_{(\,2\,)}\,=\,10\,=\,\text{A}_{(\,16\,)} \) のように書くのです。
なぜ16進法なのか? なぜ16進法だと、コンピュータが扱いやすい 数の表し方なのかというと、
16もまた、2の累乗 \(16=2^{\,4}\) です。
2進法でちょうど、\(2^{\,4}\)の位が5ビットめにありそれ未満の4ビットで表現できる状態数が 16、ということになります。
すなわち、ちょうど4ビット分が 16進数の一桁ぶんに相当する からです。
このことは、計算がしやすいということ。さらに
4ビットの「4」もまた、2の累乗でできている数です。
2進数,16進数,10進数の変換計算(整数)
ちょうど今、ふれた通り、
2進数の下から4ビット分ずつがちょうど、16進数の一桁ぶん。(2進法のときだけ「桁」のことを「ビット」と呼ぶのでした。)
したがって、2進数と16進数の変換は、難しくありません。
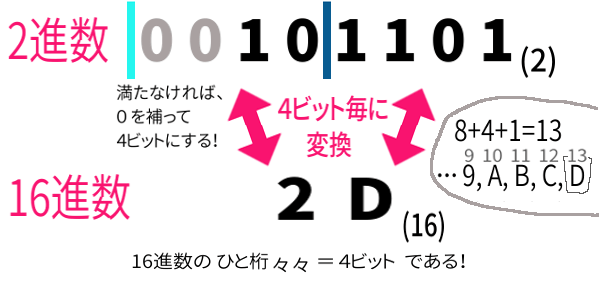
右の方にある 「 \(8+4+1=13\) 」とは、
2進数から一旦 10進数へ変換する途中計算です。
\(1101_{(2)}=8+4+1=13\) です。
この後すぐに、2進法から10進法への変換計算を述べるのですが、先に出てきた この計算だけ補足説明します。
4ビットは、右から順に 1の位, 2の位, 4の位, 8の位 となっています。
数字が1になっている位を足していくと10進数にできるのです。
だから、\(1101_{(2)}=8+4+1=13\) なのです。
(その後の計算は、16進法の 数字 を数えて言ってます。)
「4ビットごとに区切る」ということはもちろん、上の位でもまた、「1の位, 2の位, 4の位, 8の位」と数えるのであり、「16の位, 32の位, ..」とは数えません。
この記事では小数は扱わないのですが、16進法と2進法の変換は小数点以下でも同様。小数点の位置から4ビットずつ区切っていくことで、変換計算できます。
それでは、
2進法や他のn進法→10進法 の変換
を見ていきましょう。小数については → 浮動小数点数とn進小数の変換計算.. 。
まずは2進法からの変換。
先ほどのような4ビットごとに区切ることはしないで、
任意のビット数で 方法は同様です。
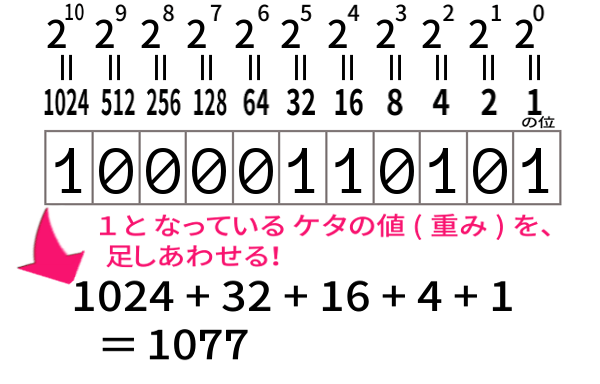
1, 2, 4, 8, … , 1024 という、10乗までの2の累乗は憶えてあるでしょうか?。
桁の値のことは 重み とも言います。
このようにして10進法に変換でき、すなわち今の例では、\(10000110101_{\,(2)} = 1077\) と言えるのです。
2進法からの変換の方法は、
「1となっている 桁の値( 重み ) を足しあわせる」と言いましたが、それは2進法では数字が 0 と 1 しかなかったため、そのような言い方になります。
数字がもっと多い、他の\(n\)進法では一般に、どうする
という言い方になるでしょうか?。
例えば8進法で見てみます。
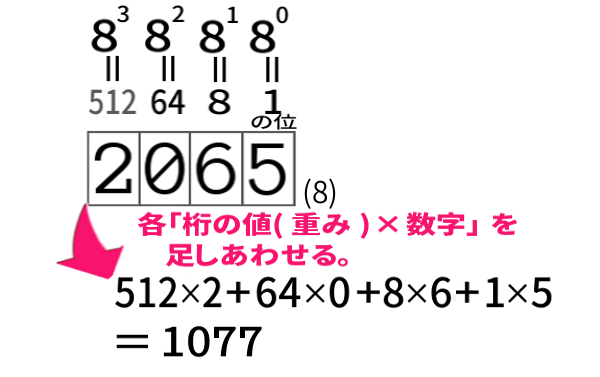
各ケタの「 重み × 数字 」を足しあわせる
という言い方になります。(同じ「1077」に相当する\(n\)進数にしました。)
そういえば10進法でも、
1077=1000×1+100×0+10×7+1×5 と表せることと同じです。
\(n=16\) 進数ではどうでしょうか?。もちろん同様ですが、
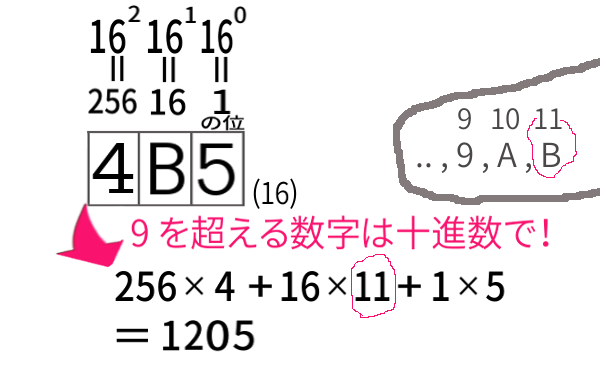
\(n>10\) の場合、9を超える 数字 も、10進法で表して計算しなければなりません。
ところで「数字」とは、何のことだったか というと、
その進法において 一桁で表される数( 一文字 )の種類のことでした。
今度は逆に、
10進法 →2進法や他のn進法 の変換
ー のやり方、例えば8進法への変換方法で、見ていきましょう。
以下の計算の結果、\(1077=2065_{\,(8)}\) が得られます。
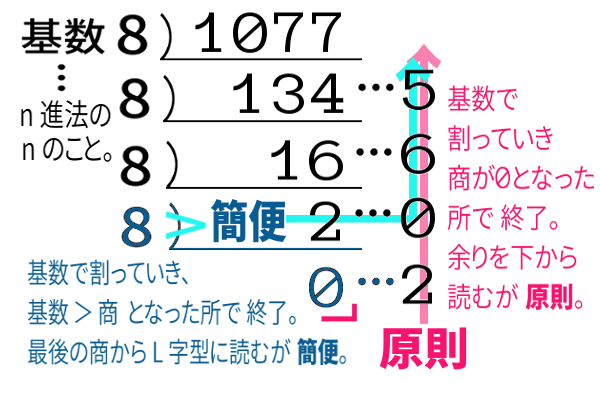
手数が1少なくなるので、簡便法の方をおすすめします。
基数 > 商 となったところで、割り算は終了です。
このように、
商を繰り返し割り算することで、
後の方の 余り ほど 上位の桁 の答となる
わけですが、その理由を考えてみましょう。
数式を使います。

出てきた商をまた、基数で割っていくということは、
数式における商を「(割る数×次の商+余り)」に 置きかえて 表していく
ことに対応しています。
だから、多くの回数割ったときに出てきた余りほど、数式で多くのカッコの中に入っていて、すなわちカッコを外せば より多くの基数がかけられている数。
いわば より上の桁の数字、ということになるのです。
そして 余り ということは、0以上 基数未満。よって、
数字 たる資格があるのです。
もしそれでも分からなければ、十進法で見てみましょう。
例えば、十進法で表した数 2345 について:
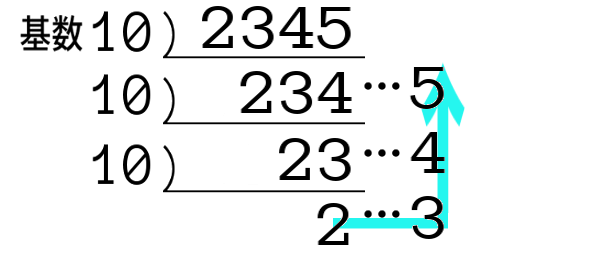
下の方から順に、各桁の数字が得られていますね。
十進法でなく、割り算の途中の数も \(n\)進法で考えればよいわけです。
とは言え、やはり別のやり方、
次のように、上のケタから比べていく方が分かりやすいかもしれません。
余った数 以下の 桁の重み のうち最大のものと比較(割り算) していく方法です。
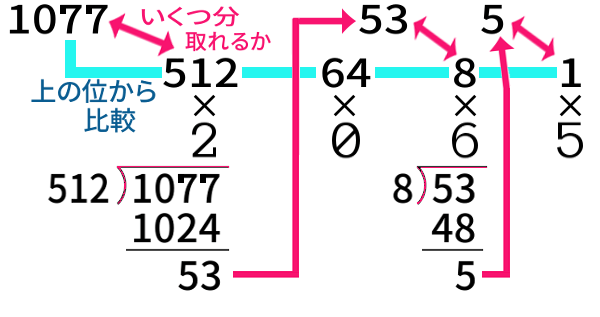
これでも、\(1077=512\times 2+64\times 0+8\times 6+1\times 5\) だと分かるので、\(1077=2065_{\,(8)}\) が求まるのですが、はじめの【簡便法】よりも計算は煩雑でしょう。
しかし2進法に限っていえば、この方法のが 簡単で分かりやすいです。
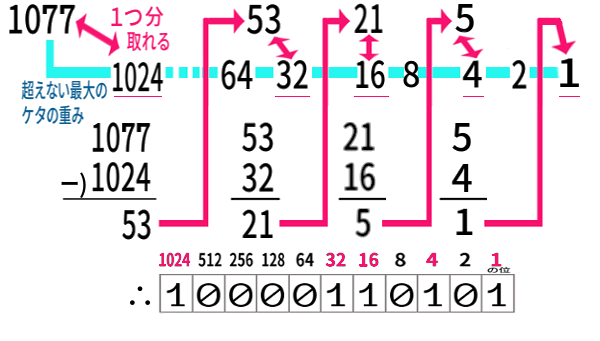
2進法では数字は、0か1。つまり、商が立つとすれば1だけで、余り(残った数) から 桁の重み を引くだけ でよいからです。
以上、10進法と \(n\)進法の変換の計算方法をまとめると、
- \(n\)進法→ 10進法 の計算方法
各「桁の重み × 数字」を足しあわせる。 - 10進法→ \(n\)進法 の計算方法
基数で割っていき、商が基数未満になった所で、
その最後の商→その余り→余りを上へ読む
【簡便法】。 - 10進法→ とくに2進法 の計算方法
上記の【簡便法】でもよいが、上の桁から、
(残りの)数 未満の 最大の 桁の重み を
引いて取り出す ことを繰り返す。
最後に1点だけ。10進法から16進法へ、一般に、
10進法から \(n>10\) の\(n\)進法へと 変換するとき。
計算方法は.. 【簡便法】ということになりますが、
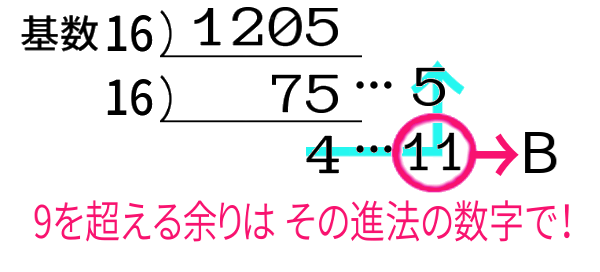
もちろん「余り」だけでなく、基数 >最後の商 >10 となる 最後の商 についても、そうです。
したがってこの例では、1205\(=\)4B5\( _{\,(16)}\) が得られます。


Enjoyed reading through this, very good stuff, regards.