補数による 負のデジタル2進数 の表現と、減法演算のしくみをわかりやすく【高校 情報Ⅰ、共通テスト向け】

コンピュータは2進数をもとにして演算を行います。
整数値0,1,2, … は2進法で数えることができますが、
( → デジタル情報の特徴~2進法 … )
それだけでなく、補数表現という方法により 負の数をも表し、扱えるのです。
このしくみについても、高校情報 Ⅰ で学習します。
見ていくことにしましょう。そのために、
2進数の復習から
詳しくは「デジタル情報の特徴~2進法 …」の記事に譲りますが、見返すのが面倒な場合、この記事を理解する、必要最低限について、再度まとめます。
桁(「ケタ」)のことを、とくに2進法の場合には「ビット」と呼ぶのでした。
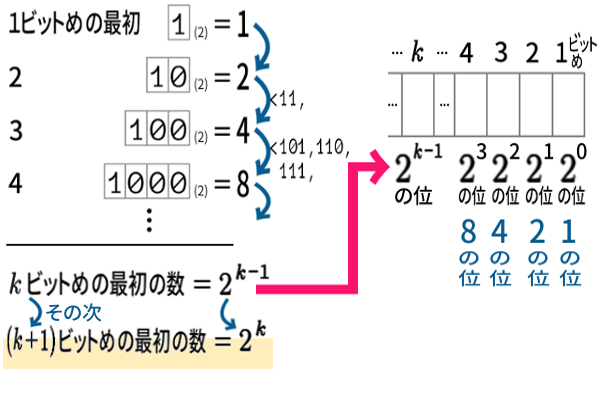
1ビットめの最初の数=1 , 2ビットめの最初の数=2 ,
3ビットめの最初の数=4 , …
それぞれ、1の位 , 2の位 , 4の位 , … と言い、kビットめの値が2の(k-1)乗 すなわち、(k+1)ビットめの最初の数 が 2の k乗 となっているのです。(ビットの番号よりも指数が、1少ないです。注意。)
ちょうど十進法で、一桁めの最初の数=1, 二桁めの最初の数=10, 三桁目の最初の数=100, … となることと同様。
いずれも、基数( n進法の「n」のことを基数と言いました。 )の 累乗( 桁数ー1乗) で表されます。
すべてのビットが1である数にも注目してみると、

ー と言えます。今までのをまとめると、

ということが分かりました。
ビットパターンなどとも言いますが、2進数はとにかく、「0」か「1」か しかない数の表し方。
とくに一方の数字しか使わない極端な例が、
「 kビットすべて1 の数」あるいは、ゼロ。そのうち、
「 kビットすべて1 の数」の値の方も大事なのです。
次もまた、ビットパターンの練習になる内容です。
補数とは何か
ある2進数の、数字「0」を「1」に,「1」を「0」に。つまり2種類の数字を 互いに逆の方にすることを、
ビット反転させる と言います。

最上位のビットが「0」だから、1010\({}_{(2)}\) と答えたくなるところですが、後にも注意を促すように、
最初のビット数(桁数) のまま 固定する(決めておく) 必要があります。
固定したビット数の中に 上の方の位で使わないビットがあれば、「0」と記すべきなのです。
この、もとの数をビット反転させただけの数を、
もとの数の補数 (「減基数(=1) の補数」) と呼ぶこともありますが通常、さらに それに1を足した数 の方が、補数 (「基数(=2) の補数」) と呼ばれます。

もとの数をビット反転させただけ が「エムスター」、
それに1を足す というのが 補数「エムバー」の計算法。
「エムバー」=「エムスター」+1 だと言えますね。
補数を求めるには2手順 ある、と憶えましょう。
ただしその前提として ビット数を 決めておくこと。既定のビット数 k に決めて、それに固定しておかなければなりません。その理由は、
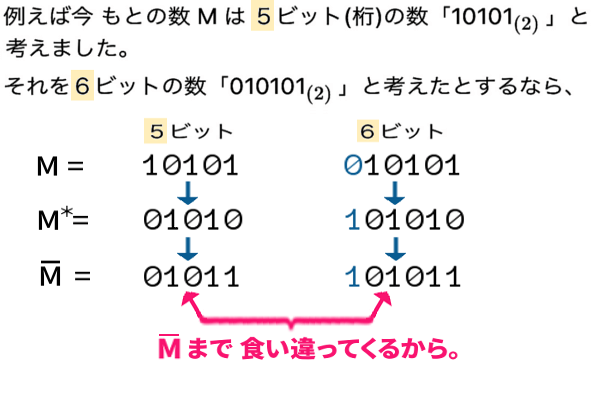
\(\dotsm\)となるからです。
最初に決めた(「既定の」)ビット数のまま固定で、その中に使わない上位のビットがあるとき そのときに限り、「0」と言わなければならないのです。
もとの数 M と、その補数との間の関係を、数式も使いながら、詳しく見ていきましょう。
足し算してみると気づくことがあります:
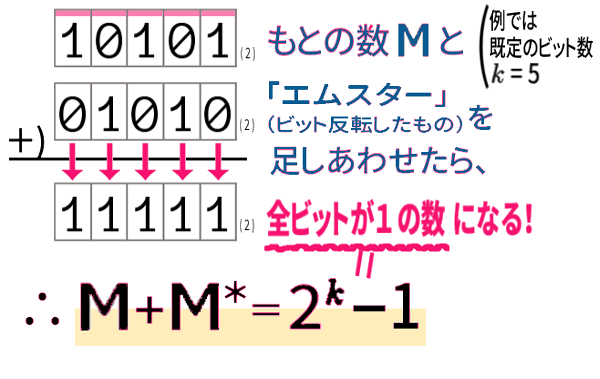
ここからさらに、「エムスター」でなく、いわゆる補数である「エムバー」との関係を見るのは難しくないです。
等式変形( 移項 ) を使って:
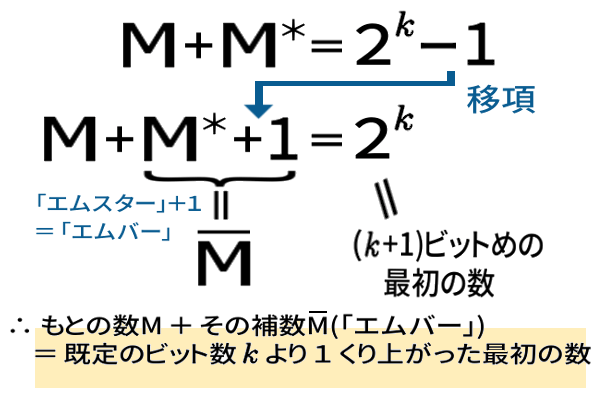
既定のビット数 k は、最初で固定してあったので、
もとの数 M も その補数「エムバー」も、いずれも k ビット(ケタ) の数。したがって、
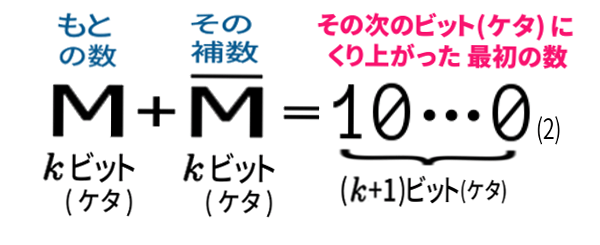
ーということが分かります。
それでも、いま一つ「補数」の意味が分からない、と思っている読者も いるかもしれません。
そこで、2進法だけでなく10進法でも補数は同様に考えられるので、見てみましょう。

いわば補数とは、「その数に足せば きっちりした数 になる」数のこと。ただし「きっちりした数」とは一桁くり上がったばかりの数。
10進法でも2進法でも、任意の n進法でも、そういうことなのです。
しかも、各ひとケタ(1ビット) ずつに分けて見てみたら、
補数は各ケタ(ビット) にも表れていて、
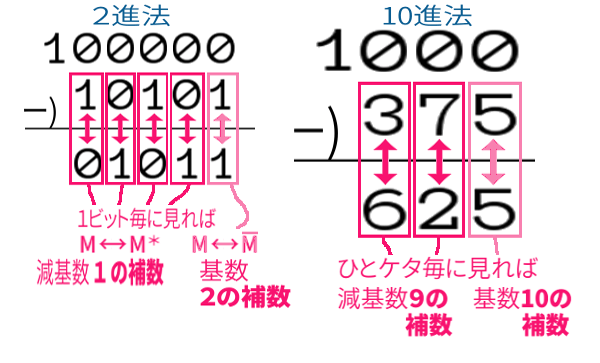
筆算やソロバンで計算するとき考えることですよね。
「1借りてくる」から 1の位以外「エムスター」です。
「減基数」という語は憶えなくても構いません。「基数ー1」の意味です。
補数「エムバー」の求め方と、性質についてまとめると、
- 補数の求め方(計算法)
既定のビット数 k をまず決めておいた上で
【1】もとの数Mをビット反転させたものに、
【2】1を足す。 - 補数の性質
もとの数 も その補数も、kビットの数で、
それらを足したものは、(k+1)ビット最初の数。
( (k+1)ビット最初の数 は 2の k乗。 )
負の整数を補数で表現する
ビット数(桁数)を 既定として決めておくこと。前提であると、前に述べました。
その理由は、前に述べたこと だけでなく 単純に、上限を既定としておかないと計算に時間もかかりますし、記憶領域も多く占有してしまうことになります。
実際、旧来からのプログラム言語では、整数型は32ビットまで、と決められてきました。
上限つまり 使えるビット数「32ビット」とはいえ、数えられる数は膨大です。累乗の式や計算に慣れていないとピンときません。
そこで話を簡単に。さらに昔のコンピュータに戻った気分で、使えるビット数が「4ビット」としてみましょう。
ともかく上限があるという点は共通。原理は同じです。
使えるビット数が 4ビット だとすると、場合の数の計算により、
2×2×2×2=2の4乗=16 通り。
「2」なのは数字が「0」か「1」か、2進法の基数、1ビット当たり2通りだから「2」です。
よって16 通りの数まで数えられるのですが、1からでなく0から数え始めるから1つ手前、2の4乗ー1(=16-1=15) まで、数えられるでしょう。

少ない数で分かってしまえば類推と数式で、使えるビット数がたとえ32ビットの場合であっても、
0 から 2の32乗ー1 までの数を数えることができると、
正しく答えることができます。
話を4ビットの場合に戻します。
今のままでは普通に、0から15までの数を表すことができています。普通なので、そこに負の数はありません。
そこで、ある解釈のルールを導入することで、0から15までの数のうちの半分を、負の数に変換してあげるようにするのです。
「ある解釈のルール」とは !? ー 先ほど述べた、補数を利用するのです。
補数表現と呼ばれます。

「変換」と言っても難しくありませんね。この変換を使って、0から15までの数のうちの半分を読み替えるのです。
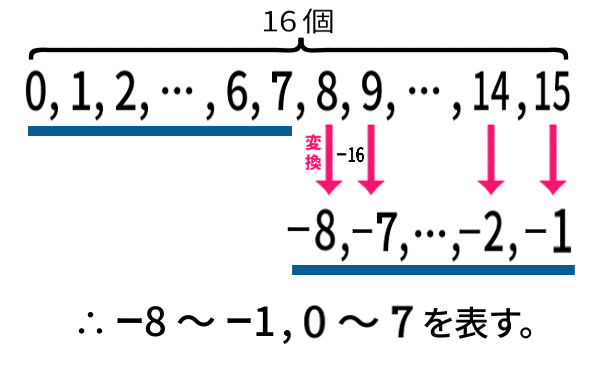
0から7まではそのままの数で、8から15までは、補数表現の変換が適用。すなわち0から15までのうち
8を境にして、数値の解釈方法を変えるのです。
「8未満か8以上か」識別するには、コンピュータ的にはどこを見るのが最適か!?ー
そこでまた2進法に注目しましょう。
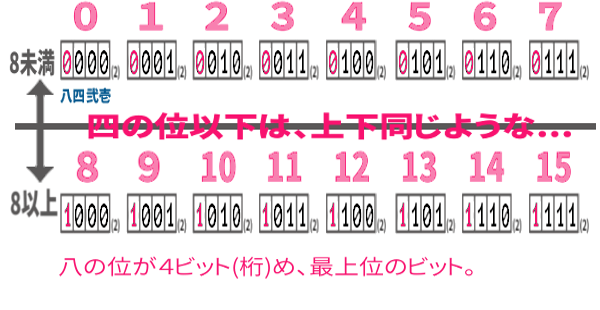
そうですね。4ビットめが「0」か「1」か、で、8未満か以上か、に分かれるのです。今は既定の( 使える )ビット数 k=4としていますので、最上位のビットです。
したがって、

一般に、既定の( 使える )ビット数=k のときでは、
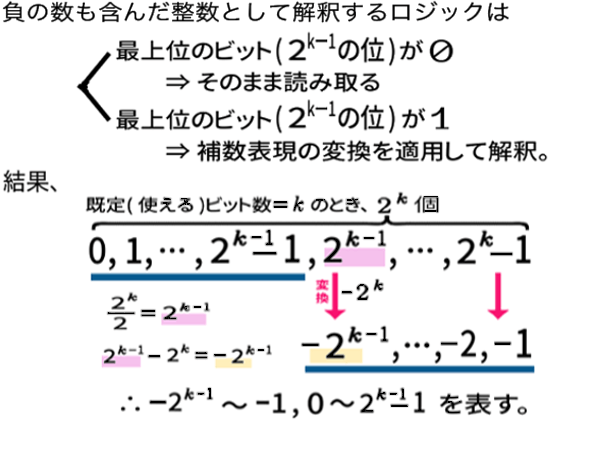
ー のように変換されるということです。
しかし「補数表現の変換」というのに
「16 (または2の k乗 ) を引く」と言って、
なぜ、補数が出てくるのか? ー それを見ておきましょう。
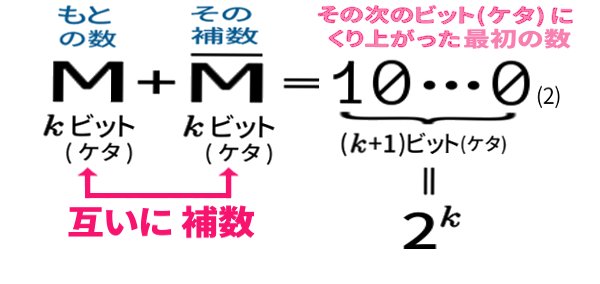
この数式が、補数の性質の代表。これをスタートにします。
実は補数の性質とは互いの関係です。つまり、Mの補数が「エムバー」であるなら同時に、「エムバー」のまた補数がMとなっています。
この数式を等式変形すると、
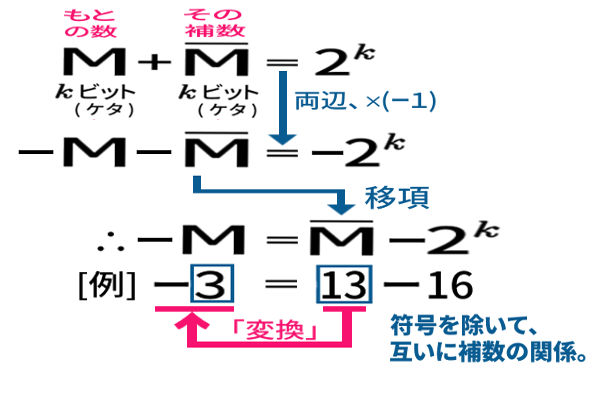
だから、16( 2の k乗 )を引くと、異符号ですが、もとの数M に対して、補数「エムバー」が現われるわけなのです。
「16( 2の k乗 )を引く」ことと
「その補数を求めてマイナスをつける」は、同じ意味 同値 ということが、分かります。
「16( 2の k乗 )を引く」ことから説明したのですが、コンピュータが実際に変換計算を行うときにはそちらでなく、あくまでも「その補数を求めてマイナスをつける」方で計算します。
実際「2の k乗」自体、既定のビット数 k で表せる数を超えており、人間に説明するときの計算方便でしかありません。
この「変換」の逆。負の数が入力されたとき、その絶対値の補数に変換する方もまた、コンピュータは行う必要があります。
そちらの方を、この記事では「逆変換」と呼ぶことにします。
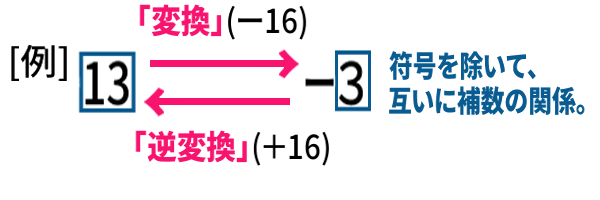
「逆変換」は「逆」ですから「16( 2の k乗 )を足す」操作ということになり、また、
「マイナスを取り除いてその補数を求める」操作と同値です。
まとめると、次のようです:

これら双方の変換を使うことでコンピュータは、正負の整数の加法( 減法 )を実行するのです。
そのしくみをさらに見ていくことにしましょう。
補数を使うことでもありますし、依然、使える既定のビット数( 上限 ) k は、決めておくこととし、とくに k=4 として説明を続けます。
補数を使った減法演算の方法
例題として、

このような減法演算の問題では決まって、
「(既定より)上のビットは無視せよ」と言われます。
本当に良いのかどうか見るのは後にして、とりあえず解答しましょう。
各項は、絶対値のみ2進数になっています。マイナスの項を補数表現に変換、つまり、
負の項のマイナスを取り除いて補数に変換するのです。
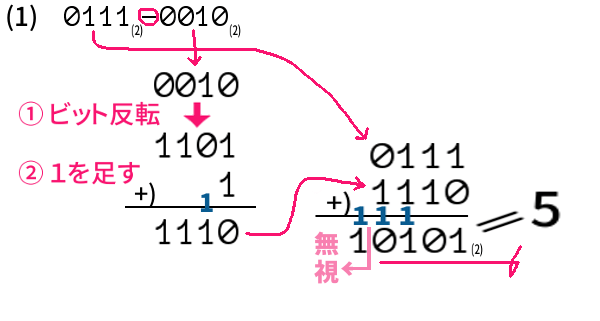
(1) ー0010\({}_{(2)}\,\longrightarrow\) 1110\({}_{(2)}\) という、逆変換つまり、
補数の求め方(ビット反転して、1を足す)を行い、
他と足し算。既定のビット数より上( 16の位以上 )は、
無視して、答を得ます。
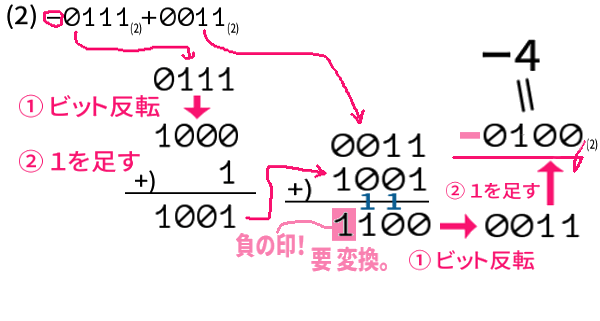
(2) ー0111\({}_{(2)}\,\longrightarrow\) 1001\({}_{(2)}\) と、補数を求め、
他と足し算。既定のビット数より上にはくり上がり
ませんが、有効な最上位のビットが「1」となるので、
負の数へと解釈する変換が最後、必要です。
最上位のビットが1( 負の印 )ならば、
補数にしてマイナスをつけるという変換です。
引き算 (減法) 以前に、
2進数の足し算 (加法) 計算のできる必要があります。
簡単にここで復習しておくと、

あとはこれら、ひと桁( ビット ) の計算の積み重ねでできます。
とはいえ、「16( 2の k乗 )を足す / 引く」という、補数変換を俯瞰したとらえ方ができるので、例題の( コンピュータがするような )計算の手順を、また、10進法で説明してみましょう:

この計算過程から、「既定より上のビットは無視」して良い理由が分かってくるでしょう。
今は減法つまり、異符号の加法演算です。
(逆)変換によって、真の答よりも16( 2のk乗 ) が足されますので、最後の変換で16( 2のk乗 ) を引くということは、もとの値が復元されるわけですから、原則として計算は正しくできます。
最後の変換の直前の値が16( 2のk乗 ) 以上の場合、2進法では16( 2のk乗 ) の位が立っているということを意味し、最後16( 2のk乗 ) を引く変換をするとは16( 2のk乗 ) の位を見ずに答を出すということですから、無視するということです。
一方、最後の変換の直前の値が16( 2のk乗 ) 未満の場合、16( 2のk乗 ) の位は立ちません。
その場合の最後の変換は、まさに補数表現の変換になるのであって、全く16( 2のk乗 ) の位以上を使う危険もなく、計算は完結できます。
したがって、いずれの場合でも、16( 2のk乗 ) の位以上を無視して良いことになるのです。
なおこの例題では、符号を取り除いた値(絶対値) の、最上位ビット(4ビットめ) はすべて「0」となっています。
既定のビット数で扱える数の範囲を守ればそうなる( 負の最小の数だけは「1」) はずです。
普通の減法計算問題でも、例題のように、補数表現を利用して答を導くことはできます。
ただし最上位ビットは「1」となっていることもありますので、その場合、既定のビット数を1つ増やし、最上位ビットが「0」となるように補正を加えて、計算する必要があります。
コンピュータが行う 減法演算(異符号の加法)の手順をまとめると、
【1】負の項の方を、補数に (逆)変換
(マイナスを取り除いて その補数を求める)
【2】他の項との間で、加法演算する
【3】桁あふれ(くり上がり等)は無視、
既定の桁の中で 必要なら補数表現の変換で解釈。
符号つき(正負の) 加法の安全性
これまで、コンピュータが負の整数を扱えるよう、補数表現というものを考えてきました。
その前提として、既定のビット数の上限を決めておく必要が出てきていました。
4ビットまでとすれば、0から15まで。負の数を扱う解釈ですと、ー8から+7まで。( 32ビットとすれば、マイナス2の31乗からプラス2の31乗マイナス1。 )
いずれにせよ、扱える数には上限下限が、厳然と存在するということです。
そこで、既定4ビットまで( 扱える数 ー8から+7まで ) のところを例えば、
12+3 などという計算はできません。
12が扱える数(7まで) の上限を超えているからです。
この場合、算式を構成するもとの各項をチェックすれば、計算を始めてはならないと分かります。
それでは7+6 はどうでしょうか?
7も6も扱える数の範囲内なので、算式を構成する各項に問題はありませんが、人が計算してみれば分かるように、答は13。計算結果は、扱える数の範囲をオーバーします。
そのような計算をコンピュータに与えても、大丈夫なのでしょうか?
もし (既定の数の範囲内で、ここまで説明したルールしか決められていない)コンピュータが、この「7+6」を計算したならば、こうなるでしょう:
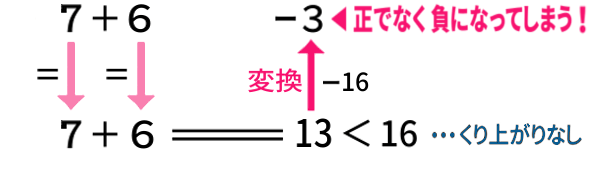
「正+正=負」となり、人間が考えて明らかな誤答を、ここで説明した範囲のルールしか実装されていないコンピュータだと、犯すことになるでしょう。
値が大き過ぎたせいで、負に変換されるべき8以上の領域に入ってしまったためです。
別の例で、ー8-3 を計算させたとしたら、どうなるでしょうか?。
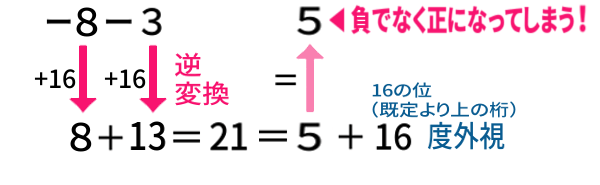
今度は値が小さ過ぎて、負に変換されるべき8以上の領域に入れなかったためです。
いずれの例も、符号がおかしくなる特徴があります。
そこで、答が範囲外となる加法演算の行われたと判定するために、

ー というロジックを追加すればよいことが分かります。
このように、演算の安全性( セーフティ ) を強化していくことも大事なのです。
加法演算の範囲を超える危険は、同符号の加法演算の場合に のみ 起こり得ると分かります。
絶対値が一方向に増大しますので。
実際、異符号の加法演算では、注意する必要はありません。
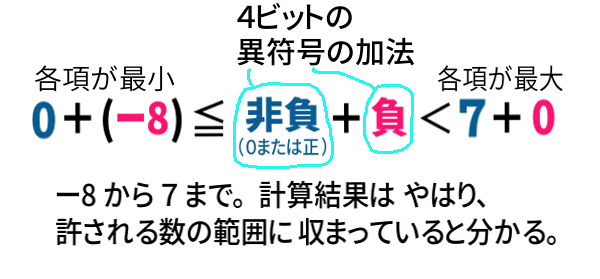
以上、既定4ビットの場合で考えましたが、32ビットなど、一般の k ビットとしても、同様の結果を確認することができます。


I¦ve read some excellent stuff here. Definitely worth bookmarking for revisiting. I surprise how so much attempt you place to make this kind of excellent informative web site.