数学的帰納法とは自然数の定義【数学の基礎, 離散数学】



● \( P(2)\) は(2cm を1回使えばよいから)成り立つ。
● \( P(n)\Longrightarrow P(n+1)\) が 成り立つ保証
つまり、\( P(n)\) が成り立ったと仮定するとき
\( P(n+1)\) が成り立つことを以下に証明。今は、
\(n\) が偶数の場合、2cmが1回以上使われている(もし例えば「6」などの場合でも、3cmばかりを使う代わりに2cmばかりを使うことが可能なので、そちらの方法で測ればよい)から、2cm1回分を3cmに代えて測ればよい。
また\(n\) が奇数の場合、3cmが少なくとも1回使われているはずだから、1回分を2cm2回分に代えて測ればよい。
よって数学的帰納法により、\(P(n)\) は2以上のすべての自然数について成り立つ。■
ーそのように証明するでしょう。
「\( P(n)\Longrightarrow P(n+1)\)」が成り立つ・正しい、ということによって、
\(n=2\) で成り立てば \(n=3\)、
\(n=3\) で成り立てば \(n=4\ \dotsm\) というように、
次、次\(\dotsm\) と、正しいことになっていき、結局すべての自然数(2以上)について成り立つだろう、と言いたいですが。
本当か? 無限回の操作は自明ではない。
「すべての」自然数と言ってしまうと、そこには無限回の操作が ともないます。
「\( P(n)\Longrightarrow P(n+1)\)」を当てはめていくのも。
確かに、\(n=10000\) でも \(n=10000000\) でも、どんなに大きな数でも、成り立ちます。有限回である限りは。
しかし、その先「すべての」数については、どこまで行ったとしても人力では、
言えたことには ならないのです。
数学の基礎を作る集合論には、選択(選出)公理というものがあります。
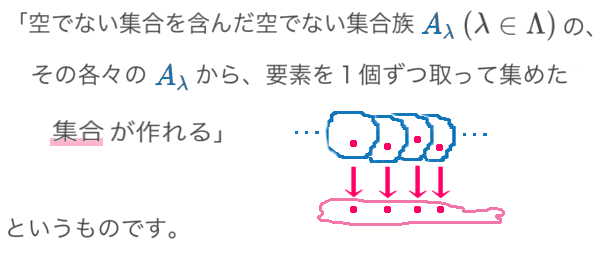
「たったそれだけのことが?」とも思えるかも知れませんが、とくに無限個の操作については、
まったく自明ではありません。
そのため、公理という形で 要請・定義することで、数学の諸理論は 支えられています。
数学的帰納法の原理である、
「\( P(n)\)が成立 \(\Longrightarrow P(n+1)\)も成立 が常に真であれば、すべての自然数 \(n\) について \( P(n)\)は成立」もまた、
自然数の公理に含めることで 要請する しかありません。
そういうわけで。
自然数とは。その定義
自然数の集合 \(\mathbb{N}\) は、次の条件(「公理」)を皆、満たすものである、と定義します:

このうちの S3 が、数学的帰納法の原理に当たるものです。なぜか。
ここで単射 \(S\) は 後続を対応させる (successor) 写像。
イメージとしては、\(0\mapsto 1\)、\(1\mapsto 2\)、\(2\mapsto 3\ \dotsm\)
ーのような、\(S(n)\,:=n+1\) だと思っておいて差し支えありません。
\(M\) が 命題関数 \(P(n)\) を満たす番号 \(n\) の集合とすると、
「 (i) \(P(0)\) が満たされる・真であり、かつ、
(ii) \(P(n)\) が真となる\(n\)に対して \(n+1\) も\(P(\cdot )\) を成り立たせる数に含まれる つまり、
\(P(n)\) が真となる \(n\,\Longrightarrow\,P(n+1)\) も真となる、という意味の仮定。これら仮定があれば、\(P(n)\) の満たされる \(n\) の集合 \(M\) は、\(\mathbb{N}\) 全体に等しい」というわけです。
「帰納法の仮定 (i) (ii) を満たす命題は、すべての自然数において成り立つ」ということは、自然数の定義に組み込まれているのです。
これら公理 (S1)~(S3) は、ペアノの公理 とも呼ばれます。(実際のペアノの公理は、多少言い回しが異なるのですが、公理 (S1)~(S3) とは同値です。)
後続写像 \(S\) と0から生成\(\dotsm\)
実は 0 から始めて、後続写像を順次適用していくことで、公理 (S1)~(S3) よりも具体的に、自然数を構成することができます。
\(0\,,\,S(0)\,,\,S(S(0))\,,\,S(S(S(0)))\,,\dotsm \)
以後、0に\(S\)を \(k\) 回適用した、\(S(S(\dotsm (0)\dotsm )\) を、\(S^k (0)\) と書くことにしましょう。すると、
\(0\,,\,S(0)\,,\,S^2 (0)\,,\,S^3 (0)\,,\dotsm \)
ですが。これらの集合を\(M\) とすれば、\(M\) は (S3) の仮定 (i),(ii) を満たすと分かります。よってこの\(M\) が、自然数全体 \(\mathbb{N}\) になると言えるのです。
公理 (S3) は、数学的帰納法の原理だけでなく、仮定 (i), (ii) を満たす集合の共通部分であるという性質を物語るものでもあるのです。
それならば、「そんな遠回しな」言い方でなく、初めから自然数を本節の言い方で定義すればよい、と思う人もいるかもですが、そうすると、数学的帰納法の論証には応用しにくくなるでしょう。
それに「\(\dotsm\)」の先はどう説明すればよいでしょうか?。
公理的な定義のメリットは、汎用性を保つことと、無限の正当化にあるのです。
それにしても気になるのは、
\( 0\,,\,S(0)\,,\,S^2 (0)\,,\dotsm\) は相異なる要素か?
ということです。
0 がまた何回か後に戻ってきて \(S^k (0)\) に等しくなるような \(k\) はないのか?
など。それも、公理から確かめることができます。
確認です。写像 \(f\) が単射であるとは、\(f(a)=f(b)\,\Longrightarrow\,a=b\) という条件を満たす写像のことでした。

\(S^{k-1}(0)\) は像なので、\(S^{k-1}(\mathbb{N})\) には含まれている数です。

したがって2つの項目から、数学的帰納法(有限回) により、証明できました。■
\(S^{k-1}(0)\) は、\(k\)回目の \(S^k (\mathbb{N})\) 以降からは もれると。
このことから、\(0\,,\,S(0)\,,\,S^2 (0)\,,\dotsm \) はそれぞれ、\(S^k (\mathbb{N})\) から もれる回めが、相異なるので、相異なる数であることが分かりました。
後続写像 \(S\) は \(n\mapsto n+1\) に限られるか?
初めに、この記事の冒頭の例題では \(n=2\) スタートでしたが、自然数の公理 (S1)~(S3) は「0」スタートです。
それでは自然数の公理は実際の問題には適用できないのではないか?ーという疑問を抱く人もいるでしょう。
その解決については簡単です。
例題の命題関数は
\(P(n)\,:=\)「 \(n+2\) cm は測ることができる」
と変えるだけで済みます。
むしろ、後続写像 \(S(n)\) を、
「 \(S(n)\,:=n+1\) だと思っておいて差し支え」ない、としたのですが、
そのような限定は、公理 (S1)~(S3) のどこにも書いてありません。
「 \(n\mapsto n+1\) の代わりに \(n\mapsto n+2\) などでもよいのでは?」
と考えられます。
もし \(n\mapsto n+2\) つまり \(S(n)\,:=n+2 \) だったとしたら、どうなるでしょうか?。
\(M\,:=\{ 0\,,\,S(0)\,,S^2 (0)\,,\dotsm \} \)
\(=\{ 0\,,\,2\,,4\,,\dotsm \} \) で、
これは公理 (S3) の仮定 (i), (ii) を満たしますので、\(M=\mathbb{N}\) とならねばならないのですが、不合理です。
自然数の公理をすべて満足させるためには、後続写像\(S\) も厳格に設定されねばならず、厳格に「次の数」に対応すべきもの、つまり、\(S\,:\,n\mapsto n+1\) に限られるべきだと、確認できました。
自然数の性質をさらに一般化すると
「整列集合」という概念へ到達します。
選出公理 \(\Longleftrightarrow\) Zornの補題 \(\Longleftrightarrow\) 整列定理
という証明にも利用される性質です。
数学的帰納法はそこでは、より複雑な整列集合における、超限帰納法に拡張されていきます。
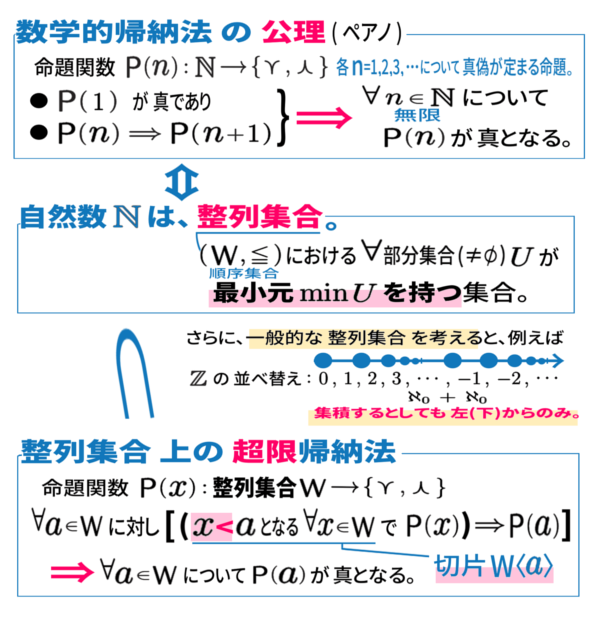
ただしここでの「数学的帰納法の公理」はむしろ、先に挙げた 公理 (S3) のように、後続写像 \(S\) による書き方をした意味においてです。
その上で、整列集合であることと同値となり得ます。
最小元も、ここでは「1」となっていますが、先に挙げた公理 の方では「 0 」に相当するもののことです。

