微分積分とは?不定積分や定積分についてもわかりやすく解説

微分・積分とは何か?【わかりやすく解説】
微分・積分とは何か?
結論からズバリ言いますと、
微分とは・・グラフの接線の傾き

積分とは・・グラフの面積の計算方法
「微分積分」と言われるのは、「微分(法)」と「積分(法)」という2種類の計算のことです。
しいてどちらの方が役に立つのか!?
といえば、正直、微分よりも積分の方が役に立ちます。
例えば、この三角形の面積は?
そうですね。正方形(長方形)の面積に注目して
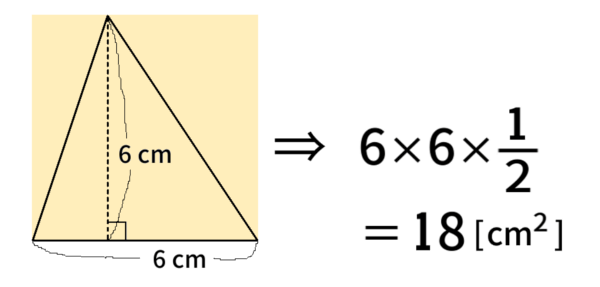
\(\dfrac{\,1\,}{2}\) をかけるのでしたね。
これはまあ分かります。確かに、半分になっていますよね。
それでは、次の体積ですが、どうでしょうか?
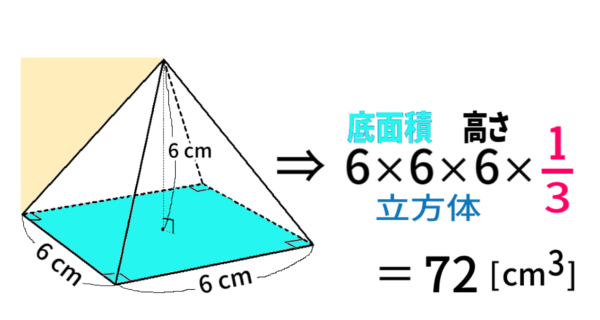
そうでした。\(\dfrac{\,1\,}{2}\)ではなく \(\dfrac{\,1\,}{3}\) をかけるのでした。
小学生や中学生の時、やった記憶がありました。
でも、どうして!? ー
その理由が実は、積分によれば、分かるのです。
「あれ、積分って体積じゃなくて『面積』って言ったよね?」
ー 言いました。しかし続けて その「計算方法」とも言いました。
「??」
ちょっと意味深。
詳しくは 身の回りにある微分積分を使った事例 で説明することにしましょう。
ともかく積分は、微分よりも役に立ちます。
ところがその計算は、三角形の面積みたいな単純計算では、できないことが普通。
そんなとき、微分の計算 を利用する 方法が 有効。
微分計算の「逆」をやれば、答えが出せるということが、実は分かってるからなのです。
… それで、まず、微分 の方から、見ていくとしましょう。
「グラフの接線の傾き」その前に
これから例えば、\(y=x^2\) のグラフを扱います。
\(y=x^2\) ってどんなグラフでしたか?
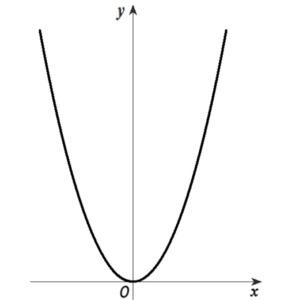
こういうグラフでした。
確か中3の最後に出てきましたね。
そもそも「グラフ」って何でしたっけ?…
グラフとは、
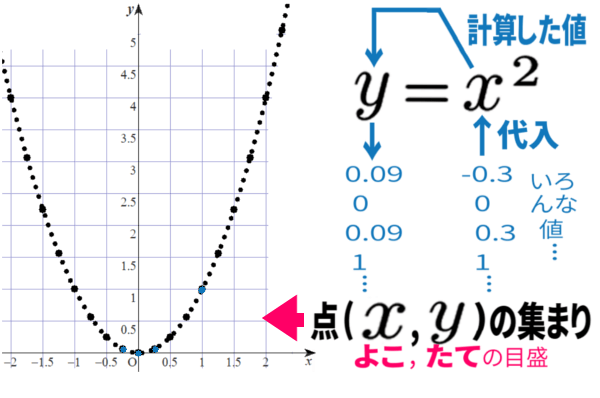
もとの 関数式(例えば \(y=x^2\) )の、
\(x\) に いろんな 値を 代入・計算、
打っていった点を つないだもの
でした。
点を打つ場所は「座標」と言い、
座標(左側の数, 右側の数)は必ず、
左側の数⇒よこの目盛 、右側の数⇒たての目盛
のように読み取って、グラフ用紙に記入する約束でした。
左右逆にしないよう、気をつけておきましょう。
一般に「\(y=x^2\)」以外の式。例えば
「\(y=x^3\)」とか「\(y=x^3 +2x^2 -1\)」などでも、
同じようにやれば、
グラフをかくことができます。
\(y\) の値を決めるのは それら 式の右辺。\(x\) の式だから、
それを記号で \(f(x)\) などと表します。
「関数 \(f(x)\,\)」、「グラフ \(y=f(x)\,\)」という
言い方をします。
グラフをかくときには、大事な約束事があります。
いろんな値を代入していく方の変数 \(x\) は、よこの目盛り 、
計算して値が決まる方の変数 \(y\) は、たての目盛りで表す
という約束です。
すなわち、
よこの目盛り \(x\) がいろんな値を変化するとき、それにあわせて、たての目盛り の値 \(f(x)\) が どう変化するかを表したものが、関数のグラフ
ー ということになります。
中学~高校数学では、よこの目盛りが大体は \(x\) で、関数の式は \(x\) を使って表しますが、理科(物理)では、よこの目盛りを時刻 \(t\) にすることが多いですね。
… 微分の話へと進めましょう。
微分とは、グラフの接線の傾き
微分とは「グラフの接線の傾き」です。
例えばグラフ \(y=x^2\) 上の一点、例えば A\((1,\,1)\) に決めて、接線を引いてみます。
接線とは、グラフの曲線と1点だけでかする(1点だけを共有する)直線。
まずは定規でうまい方向を 見つけるやり方で、引けます。
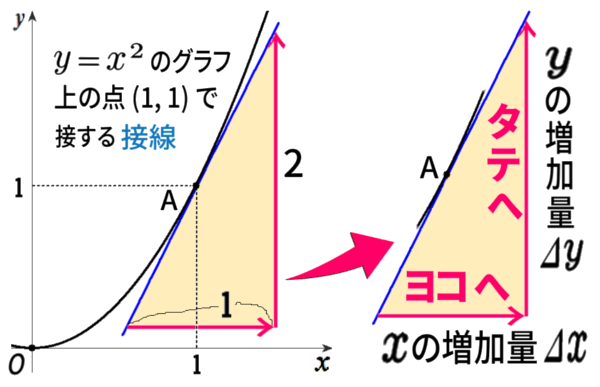
接線が引けたら、\(x\) 軸と平行につまり ま横に、1の長さをとり、
次に \(y\) 軸と平行 つまり縦に、長さを計ってみます。
長さを計ると、2です。
これで傾きが求まります。
「傾き」とは何だったか 復習しておくと、
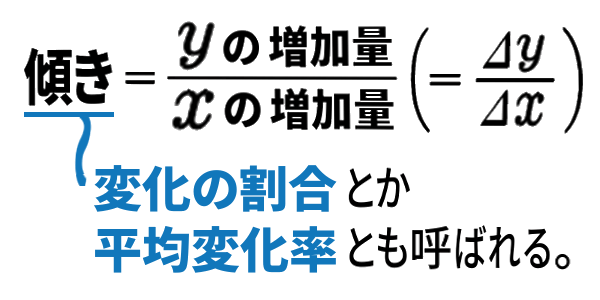
ここで記号を使いました。「\(x\) の増加量」「\(y\) の増加量」を、「デルタ」という文字を頭につけて、
「\(\Delta x\) 」「\(\Delta y\) 」と書き、「デルターエックス」「デルターワイ」と読みます。
「\(\dfrac{\Delta y}{\Delta x}\)」と書いたからといって、「\(\Delta\)」で約分して「\(\dfrac{y}{x}\)」と
することは できません。
あくまでも「\(\Delta x\)」、「\(\Delta y\)」は一かたまりで一つの文字。
「\(\Delta\)」かける「\(\,x\,\)」や「\(\,y\,\)」の意味ではないのです。
計算にもどって、今の傾きは、
\(\dfrac{\,2\,}{1}=2\)と出るので、
これで1つ、微分が求められました。きちんと言い表すと、
関数 \(y=x^2\) 上の点 A\((1,\,1)\) における微分係数は2である
ーとなります。
略して「微分」でよいのですが、正式には「微分係数」と言います。
理科(物理)では、よこの目盛りが時刻 \(t\) なので、
微分係数つまり接線の傾きは、「瞬間の速度」
という意味になるでしょう。
他の点についても微分
つまり、接線の傾きを調べてみましょう。
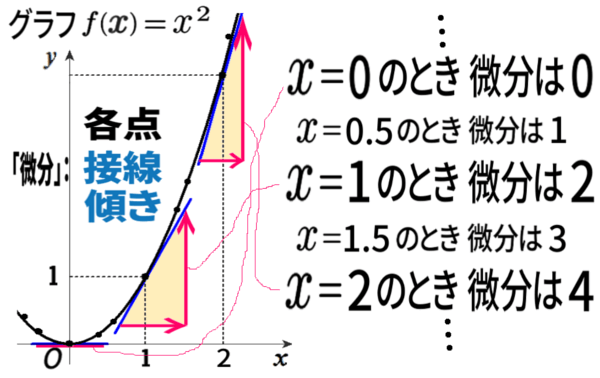
\(x\) の値の2倍の値になっている、つまり、値 \(x\) のとき \(2x\) と分かります。
各 \(\,x\) の値に対して \(2x\) の値が対応するわけなので、これも関数。
\(y=2x\) と書いてもよいですが、そうすると
もとのグラフだった \(y=x^2\) と、左辺が同じ \(y\) ではゴッチャになってしまいます。
もとの関数 \(y=x^2\) から、別の関数式が「導かれた」わけだから、
\(f(x)=x^2\) に対して \(f\,’\,(x)=2x\) と書き
「導関数」とか「微分した関数」
と言います。
「\(f\,’\,(x)\)」は「エフ ダッシュ X」と読みます。
「エフ プライム X」と読む人もいます。
\(y\,’\)(「ワイダッシュ」)という記号もよく使います。
「 関数 \(f(x)=x^2\) を微分すると \(f\,’(x)=2x\,\) 」,
「(もとの) 関数 \(y=x^2\) の導関数は \(y\,’=2x\,\) 」、
などと言えます。
関数記号「\(f\,\)」を使わずに、
$$\Large{(x^2)\,’=2x}$$
のように書くこともできて、これがいわゆる
「微分の公式」です。
この「ダッシュ」記号によれば、
関数 \(f(x)=x^2\) 上の点 A\((1,\,1)\) における微分係数 \(f\,’(1)=2\) である
ー と言い表せます。つまり、
当初一点 A\((1,\,1)\) いわば \(x=1\) のとき だけ に注目して 値を求めたことが、いろいろな実数 \(x\) に対する値がもう既に分かっていて、特定の値 \(x=1\) のときは代入で簡単に求められることになったのです。
今度からは、「2」という答えを出すとき、
「関数 \(f(x)=x^2\) を微分すると \(f\,’(x)=2x\) だから \(x=1\) を代入、\(f\,’(1)=2\ \ .\) 」
というように、公式代入で、すぐ出せるようになります。
他の関数式についても、微分の公式はあります。
それぞれの関数のグラフで、いろんな点における接線の傾きを調べていけば、先ほどと同じように求めることが可能です。
\((x^0)\,’\) つまり \((1)\,’\,=0\) , \(\quad (x^1\,)\,’\,=1\) , \((x^3\,)\,’\,=3x^2\ \dotsm\) が成り立ちます。
まとめると、
$$\Large{(x^n)\,’=nx^{\,n-1}}\ \ (n\text{は整数})$$
その他にも、知られている公式として、
$$\Large{\{a\,f(x)\}\,’=a\,f\,’(x)\quad}$$
定数倍は どけて計算すればよい という意味ですね。
以上、微分とは、
もとの関数のグラフの各点における接線の傾きであり、
公式によって計算で 簡単に求められること まで、
見てきました。
「そもそも なぜ『接線の傾き』なのか」
という疑問には、微分の定義をしっかり のところで答えます。
積分とは、グラフの面積の計算方法
微分の話はいったんそれくらいにして、積分の話に入りましょう。
積分とは、グラフの面積の計算方法です。
まずは単純な形のグラフの復習です。
このグラフの関数式は、何でしょうか?。
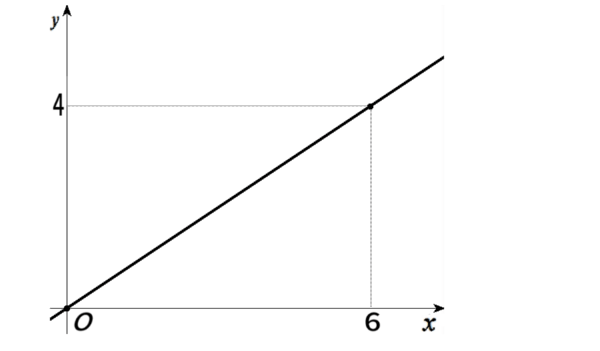
ー そうですね。\(y=\displaystyle \frac{\,2\,}{3}x\) です。
原点 O を通る直線は \(y=mx\) という形の (関数)式。
「比例のグラフ」とも言われました。そこで、
傾き \(m=\dfrac{\,4\,}{6}=\dfrac{\,2\,}{3}\) だからです。
\(f(x)=\dfrac{\,2\,}{3}x\) と書いてもよい。
では、次の面積はいくつでしょうか?:
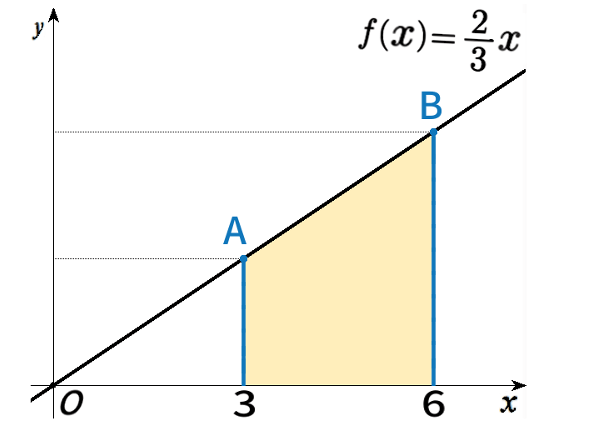
\(y=\dfrac{\,2\,}{3}x\) に代入して分かるように、点Aの高さ( \(y\) 座標)は2、点Bの高さ( \(y\) 座標)は4。台形で、「たて」の長さの方を底辺(上底、下底)と考えて、

「インテグラル 3から 6までの \(\displaystyle \frac{\,2\,}{3}x\) ディーエックス」
と読みます。
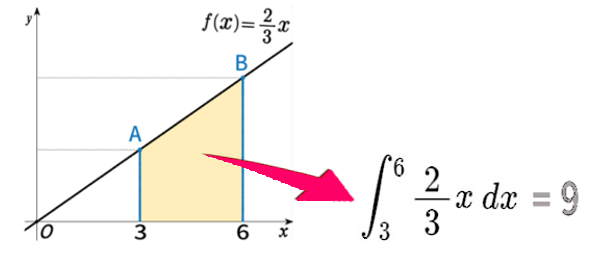
このように面積を式で表す、それが 積分 なのです。
「インテグラル」と続きの記号は どういう意味か !? :
それは、
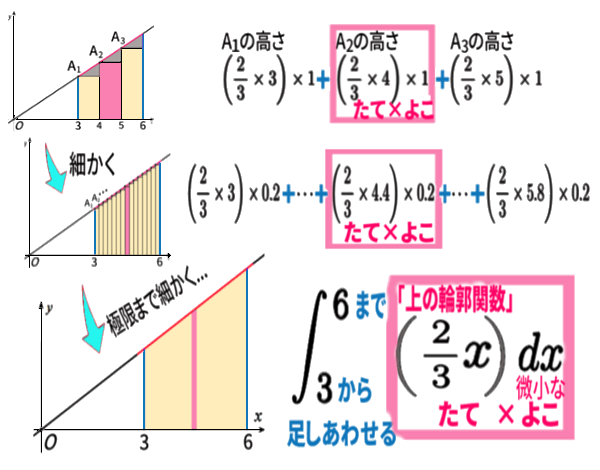
切り方を細かくしていくほど、実際の面積との誤差というかズレが、だんだん小さく、ゼロに近づいていきますよね。
その到達するであろう 極限 において
よこの長さが微小な 細長い長方形を全て
足しあわせる
という意味なのです。
グラフが上側の境界線になっているので
「上の輪郭関数」という名前で呼ぶことにしましょう。(正式名称ではありません。)
今の「上の輪郭関数」は、\(y=\dfrac{\,2\,}{3}x\)です。\(f(x)\) です。
細長い長方形。一つぶんを拡大してみると、こうです↓
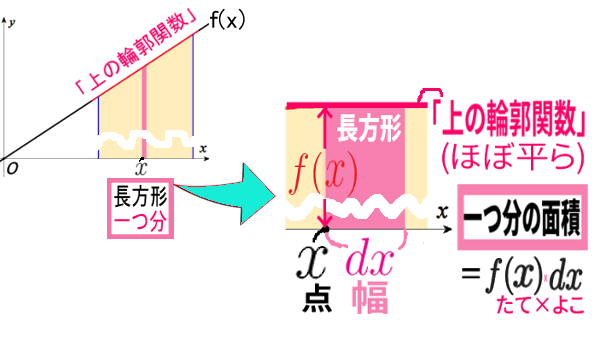
よこは微小な長さ \(dx\) とは、
よこの増加量 \(\Delta x\) の、ゼロに近い極限として表した記号。
これも「 \(\Delta x\) 」と同様、
「 \(dx\) 」の「\(d\)」と「\(x\)」は分けられない、一塊で一つの記号です。
\(x\) は一点(位置)を表し、\(dx\) は 幅(増加量)を表す、
\(x\) と \(dx\) は別々の記号。例えば
「 \(x=3\) の位置から 微小な長さ \(dx\) だけ進む」
のような意味で使います。
よって、長方形一つ一つの面積が、たて×よこ\( =f(x)\,dx \) 。
そのような長方形が 横方向に集まっていて、足しあわせたものは、
グラフとの間の面積になっている、という考え方です。
今は「上の輪郭関数」が 直線 \(f(x)=\displaystyle \frac{\,2\,}{3}x\)でしたが、
\(f(x)\)が一般の関数、曲線であっても同じように考えれば、やはり実際の面積とのズレは、ゼロに近づいていくでしょう。
「上の輪郭関数」\(f(x)\) は曲線でも何でも 構いません。
以上で見た、積分の記号の意味をまとめておきます:
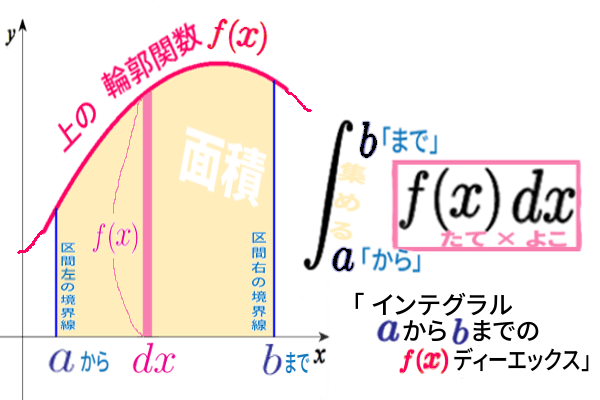
言い忘れました。区間の計り始めの数 \(a\) は、インテグラル記号の下の方に。
区間の計り終わりの数 \(b\) は上の方に書きます。
「から」の数はインテグラルの下、
「まで」の数は上
と憶えておきましょう。
積分は面積の計算方法ですが、注意点
「積分は面積」と言ってきました。しかし通常の面積の計り方と異なる点も出てきます。みていきましょう。
先ほどのグラフを使って。まず、この積分の値はどうでしょうか?:
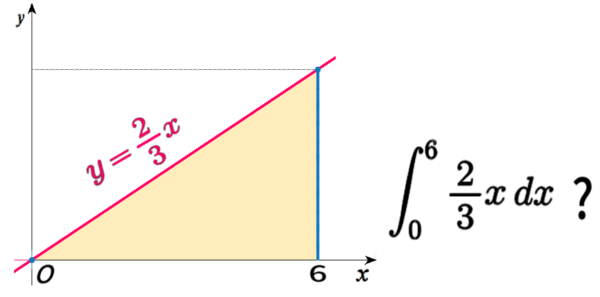
これは三角形の面積ですね。区間左側の境界線は一点になって見えます。だから、
$$\displaystyle \int_{0} \!\!\!\!\! \phantom{l^{\int}}^{6} \frac{\,2\,}{3}x\,dx\, \left( =6\times 4\times \frac{\,1\,}{2} \right) =\mathbf{12}$$
です。
では、次の積分はどうでしょうか? \(x\) が \(-3\) から 3 まで です:
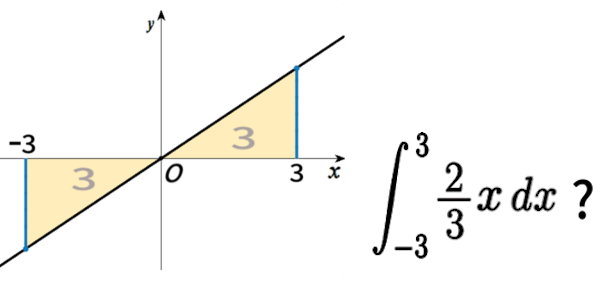
答えは両方を足した、3+3=6 でしょうか?
実は0になるのです。
積分で計る面積とは、「符号つき」すなわち、
よこ軸よりも 下で測る面積の分は、負(マイナス)の数となって
数えられるのです。
積分と、通常の面積の測り方は、その所が異なります。
$$\displaystyle \int_{-3} \!\!\!\!\!\!\! \phantom{l^{\int}}^{\!3} \ \frac{\,2\,}{3}x\,dx\, =-3+3=\mathbf{0}\ .$$
なぜ \(x\)軸より下で測ると マイナスになって数えられるか、理由をみておきましょう。
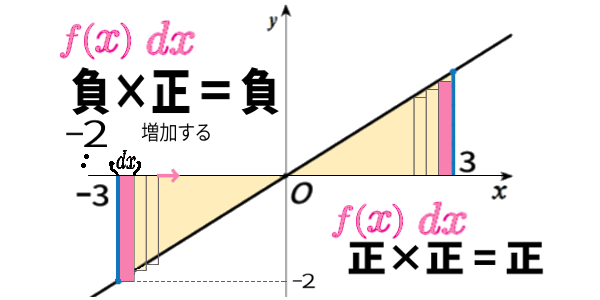
グラフが \(x\)軸より下に潜りこんでいる所。原点Oよりも左の領域では、\(f(x)\)の値は、負の数になります。
\(x=-3\) の所での\(f(x)\)の値 \(f(-3)=-2\) になるなど。
積分とは、長方形の面積=たて×よこ、
というよりもむしろ、
\(f(x)\times dx\) の値を足しあわせた総和なのでした。
言わば「たて」に相当する\(f(x)\)の値は、正の数ならばきちんと面積を表しますが、負の数だと、面積にマイナスをかけた負の数として計算するのが積分なのです。
ただし「よこ」に相当する \(dx\) は正の数。\(dx\)とは増加量で、今の場合\(x\) は\(-3\) から\(3\)まで変化するので増加し続ける、正です。
したがって、グラフが \(x\)軸より下に潜りこんでいる領域では、積分は負の値になるのです。
積分とは、グラフと横軸との間の 符号つき 面積の値
と言えるでしょう。
グラフのことを「上の輪郭関数」とも言いました。
「上の」と強調したのはこういう理由で、
もし「下の」輪郭になっていたら、その分の面積は、積分の値と 異符号 なのです。
不定積分と定積分の違いとは?
今までの積分は実は、「定積分」というものになります。
左右とも境界線が定まっていた、つまり
\(x\) の値が、「から」の数 \(a\) と「まで」の数 \(b\) の間と
決まっていました。
それに対し、左の境界線(「から」の数)は決めておく・固定しておきますが、
右の境界線(「まで」の数)を、変数 \(x\) として 変化させてみます。
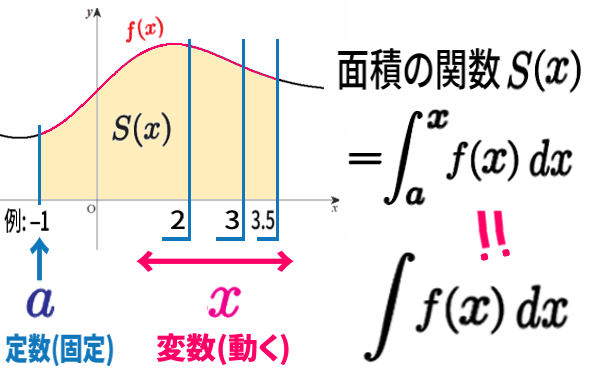
例えば、\(a=-1\) に固定しておき、
\(x\) を2,3, … など変化させたとき、\(x=2\) のときの値 \(S(2)\) は、-1から2までの間のグラフより以下 の部分の面積。例えば、7.2くらい、
\(x=3\) のときの値 \(S(3)\) は、-1から3までの間のグラフより以下 の部分の面積。もう少し広くなって例えば 9.8 … というように。
\(x\) の値が 変化するのにあわせて、\(S(x)\)の値も変化するという、「面積の関数」になります。
これを不定積分と言います。\(x\) が自由に変化するので
インテグラルの所にあえて書かず、
$$\ \Large{\displaystyle \int\,f(x)\,dx}$$
のように書きます。
実はこの不定積分で考えると、
「積分は微分の逆である」ことが 証明できます。
そうすると、初めの例のような三角形の形に限らず、
曲線 になっているグラフ と よこ軸 との間の面積であっても、
計算で答えを出すことができるようになるのです。
「積分は微分の逆」を明らかにするため、微分の定義しっかり
そのためには、微分の方も、考え方をさらに整備しましょう。
「微分」とは、何でしたっけ⁉。
グラフ上の各点における接線の傾き、でした。
そのときグラフ上の一点に注目して、そこに接線をひくことを、グラフ上に作図していました。
その接線をひこうと作図するとき、どういうことに気をつけますか?。
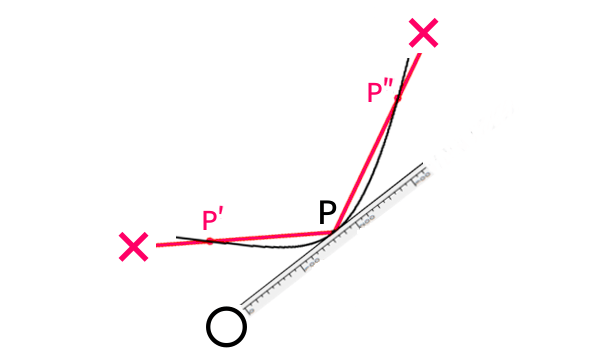
そうですね。接線とはその点で「かする」直線だから。
傾きが少しでも大きかったり小さかったりすれば、
その点以外のもう1点すなわち、
2点で交わってしまう ‼
逆に言うと、
2点で交わった状態から、注目する点P以外の方の点をPに向かって近づけていくと、接線の傾きつまり、微分の値となる。
このことを式にしてみましょう。
2点で交わったある状態がスタートで、接した状態がゴール。
2点で交わるとき、2点を結ぶ直線の傾きを、
「変化の割合」または「平均変化率」と呼びます。

それでは、点Pともう1点。2点で交わった状態から、P以外の方の点を、Pに向け近づけていったときの行き先を、表す式です。
点Pの よこの目盛りが \(x\) としましょう。
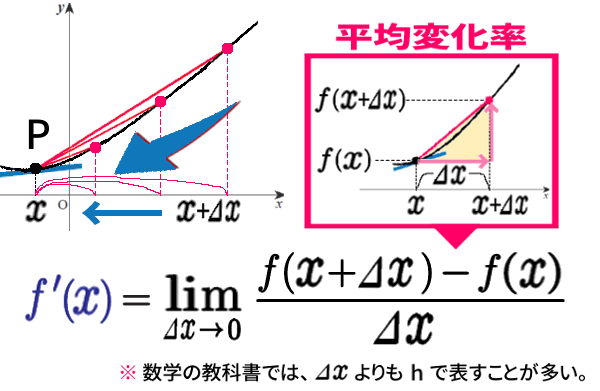
「lim」と書かれた記号は「リミット」と読み、近づけたときの行き先の値。極限値を表します。
「2点の差\(\Delta x\) をゼロに近づけたときの、平均変化率の極限値」
という意味です。
\(x\) の増加量 \(\Delta x=(x+\Delta x)-x\) です。差です。
\(y\) の増加量 \(\Delta y=f(x+\Delta x)-f(x)\) 、やはり 差。
だから「lim」の続きの式は、平均変化率を表しています。
差を計算するときは 必ず、
「変化した後の値」から「変化する前の値」を引き算
するようにします。気をつけましょう。
この式が、微分をきちんと計算で出すための式。「微分の定義」というものなのです。
\(\displaystyle \lim_{\Delta x\to 0} \frac{\Delta y}{\Delta x}\)とも書けるので、\(f’(x)\)以外にも微分は
「 \(\displaystyle \frac{dy}{dx}\) 」 という記号も よく使います。
微分の定義 からは、すべて計算することができます。
実は、先ほどの \((x^2)\,’=2x\) なども。
その計算練習は 問題編 のところに回して、とりあえず進みましょう。
ともかく「微分の定義」の式の形だけ、印象に残しておいてください。
「積分は微分の逆」の理由、いよいよ
行ってまた戻ったりで少し混乱するかも ですが、また積分の話です。
積分とは… 「グラフの面積」でした。
積分のうちとくに不定積分の方を考えていきます。
「不定積分」とは…「グラフの面積の関数」でした。
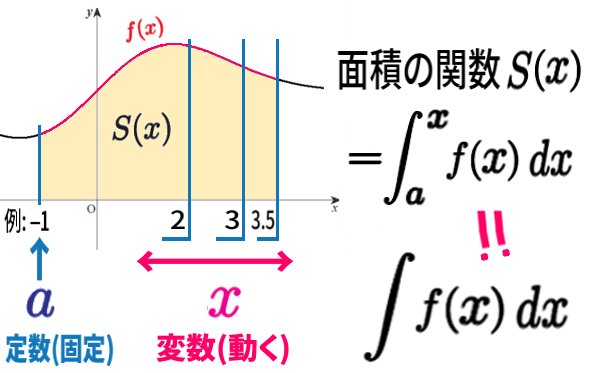
この、グラフの面積の関数 不定積分で、\(x\)から \(\Delta x\)だけ、少しだけ、変化させてみます。
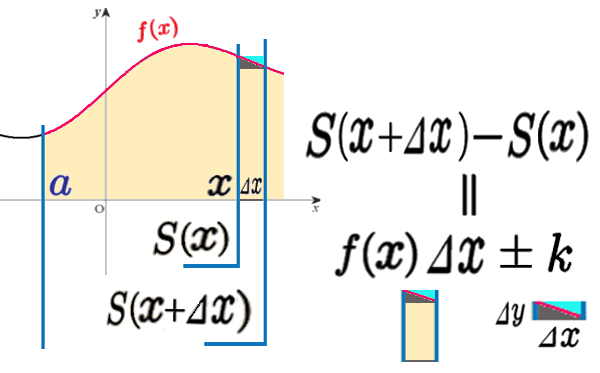
「\(f(x)\,\Delta x\) 」は、やはり「たて×よこ」。長方形です。
\(\Delta x\) は、まだ \(dx\) ほど小さいわけではありません。
「 \(k\) 」は正かもしれませんし、負かもしれません。\(y\) の増加量\(\Delta y\) は、グラフの高さの差 \(f(x+\Delta x)-f(x)\)ですが、グラフが増加ではなく減少すれば、\(\Delta y\) は負になるからです。
負になるかもしれないという意味で、「プラスマイナス」という記号で書いておきましたが、\(k\) は正でも負でも良いので「+」だけで構いません。
次に、この 出てきた等式の 両辺を \(\Delta x\)で割ってみましょう。
そのあと、\(\Delta x\) を \(dx\) にしてみるつまり、小さくして0 に近づけていってみましょう。

すると、左辺に見えてきた式は何でしょうか?
そうですね。
少し前にやった、微分の定義の式の形ではないですか?。
「\(f\)」が「\(S\)」に変わっただけで。
「\(S\,’(x)\)」と表すことができます。
ここで近づく・動く変数は \(\Delta x\) だけです。
\(x\) は、任意の値ですが、今は動かずある値のまま止まっています。だから値「\(\,f(x)\,\)」も止まったまま。今は定数。
近づいたり動いたりしないから「\(\,f(x)\,\)」に「lim」はつきません。
\(\displaystyle \lim_{\Delta x\to 0} \frac{k}{\Delta x}\)はゼロです。
つまり、\(\dfrac{k}{\Delta x}\)は、\(\Delta x\)をしぼっていったとき、ゼロに近づきます。「 \(k\) 」とは何だったかというと、面積の関数 \(S(x)\) と \(S(x+\Delta x)\) の差をとったときの、灰色や空色(半々)の長方形の面積でした。
(長方形の面積)\(=\Delta x\times \Delta y\) で、\(\displaystyle \frac{k}{\Delta x}\)は、ほぼ\(\Delta y\) ということになります。\(\Delta x\)をしぼって0に近づければそれに合わせて、\(\Delta y\) もゼロに近づきます。(きちんと言うと「連続関数」の性質です。)
したがって、\(\displaystyle \frac{k}{\Delta x}\)は、\(\Delta x\)をしぼっていったとき、ゼロに近づくと分かります。
最後の10行くらいがもし分からなければ、
「\(S(x+\Delta x)-S(x)\) は 大体 \(f(x)\,\Delta x\) に等しい」
でかまいません。
そういうわけで、
$$\Large{S\,’(x)=f(x)}$$
つまり
不定積分という面積の関数を微分したものは \(\,{\mathbf{f(x)}}\)
ということが言えて、
積分は微分の逆
つまり記号で言えば
\(\displaystyle \int\,f(x)\,dx = S(x)\) で、\(f(x)\) は \(S(x)\) の微分
だということが、これで分かりました。
積分の計算を確立する
そうすると、積分の計算は、
微分の逆である不定積分 を活用すれば、できる ということになります。
これから逆をやらなければならないので、上のほうで見た微分の公式を復習しましょう。
\((x^2 )’=2x\)、\((x^3 )’=3x^2\) 、… などでしたね。
このうち \((x^3 )’=3x^2\) で見てみると、
●「\(x^3\) 」の微分が「 \(3x^2\) 」で、
● \(\displaystyle \int\,f(x)\,dx = S(x)\) で \(S(x)\) の微分が \(f(x)\) .
ということなので、
\(S(x)\) を \(x^3\) 、\(f(x)\) を \(3x^2\) とすれば(代入すれば)、インテグラルを使った式で こうではないか !? ー
$$\text{「}\ \ \int\,3x^2 \,dx=x^3\ \ \ \text{」}$$
ー しかしこれは 正解とは言えません。
微分の「逆」をやろうとしてるのですが 注意点があり、それは
「本当にただ一通りだけなのか?」
ということです。今の例で言うと、
「微分して \(3x^2\) になるのは本当に \(x^3\) だけなのか?」
ということです。
そうではありません。
\(x^3 +1\) も \(x^3 +2\) も \(x^3 +3\) も、微分すると確かに皆、\(3x^2\) になります。足されてる定数を微分したら皆ゼロになってしまうからです。
何通りもあるのなら、それらすべてを 答え としなければなりません。
そこで正確には
$$\int\,3x^2 \,dx=x^3 +C\ \ (C\text{は積分定数})$$
と表すべきです。積分定数 \(C\) は任意の実数です。
一般に、
$$\int\,f(x) \,dx=F(x) +C\ \ (C\text{は積分定数})$$
ここで \(F\,’(x)=f(x)\)
と言うことができます。
今後、「\(S(x)\)」よりも「\(F(x)\)」を記号として使っていきます。
積分定数 \(C\) の意味についても考えておきましょう。
不定積分の意味とは? ー 面積の関数 でした。
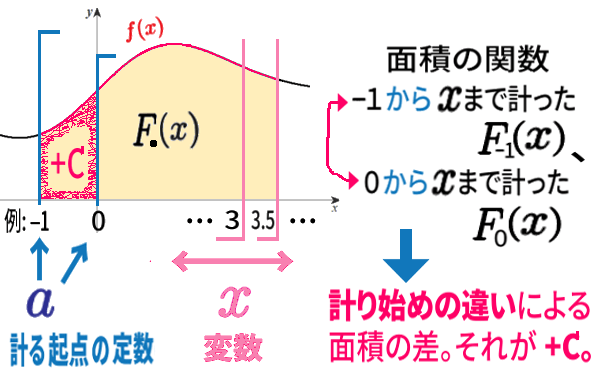
不定積分は\(\displaystyle \int \,f(x)\,dx\)とだけ書かれましたが、詳しくは\(\displaystyle \int_a \!\!\!\!\! \phantom{l^{\int}}^x f(x)\,dx\) :起点 \(a\) から、\(x\) までの範囲で計った グラフの面積の値 でした。その計り始め、起点 \(a\) が例えば、\(-1\) だったときの面積の関数と、0 だったときの面積の関数では、永久に、計り始めの違いによる面積の差がついたままです。
それが \(C\)(または\(+C\))の意味なのです。
不定積分をするときには、どこでもよいが必ずどこかに計り始めの起点がある、と頭の片隅に意識して、必要なときには忘れず「\(+C\)」をつけるようにしましょう。
今 分かった、不定積分の計算を振り返っておくと、
$$\int\, 3x^2 \,dx = x^3 +C\ \ (C\text{は積分定数})\quad\quad$$
です。微分の逆だから。そして\(+C\)を忘れないこと、
でした。
ついでにもう少し。
もっと単純な、「\(\displaystyle \int \,x^2 \,dx\)」が知りたいですよね。
つまり、微分したら \(x^2\) になる関数。どうすればよいでしょう。
微分の公式では\((x^3 )\,’=3x^2\) でした。
難しくありません。両辺に逆数をかければ解決です。
\(\displaystyle \left( \frac{x^3}{3} \right)^{\!\prime}=x^2\) だから、
\(\displaystyle \int \,x^2 \,dx=\frac{x^3}{3}+C\ \ (C\text{は積分定数})\)
となりますね。
それではいよいよ、グラフの面積の両端が定まった、定積分 の計算方法を確立しましょう。
不定積分を使用していきます。
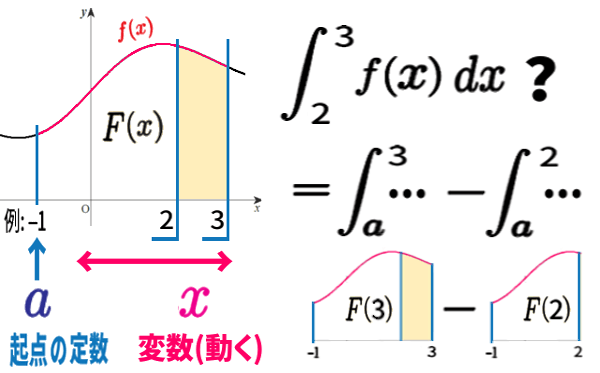
例えば、「2から3までの面積」を求めたいとき。
一方、不定積分とは任意に起点 \(a\) を固定して、
「起点 \(a\) から \(x\) まで」でした。通常は \(a\) は、定積分のいずれの今の端点(2または3)とも異なってかまいません。例えば \(a=-1\)とか。
それならば、どうしても起点 \(a\) から計りたかったとしても、
「起点 \(a\) から右端のほう(3)までの面積」から
「起点 \(a\) から左端のほう(2)までの面積」を引き算する、
ーという計算をすれば、解決です。つまり、
\(\displaystyle \int\, f(x)\,dx=F(x)\) としたとき、
\(\displaystyle \int_2 \!\!\!\!\! \phantom{l^{\int}}^3 \, f(x)\,dx=F(3)-F(2) \)
ーと計算していけばよく、さらに大かっこで \(\displaystyle [\,F(x)\,]_2 \!\!\!\!\!\! \phantom{l^{\int}}^3 \)
のように途中、表すことが多いです。結局
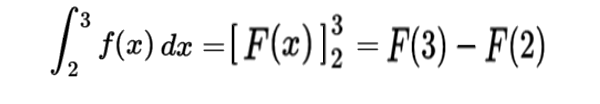
のように書いて、計算を進めるようにします。
右端のほうの数は「まで」の数、左端のほうの数は「から」の数、とも呼びました。
今ここで、確立した定積分の計算を、1つ例題で練習してみましょう。
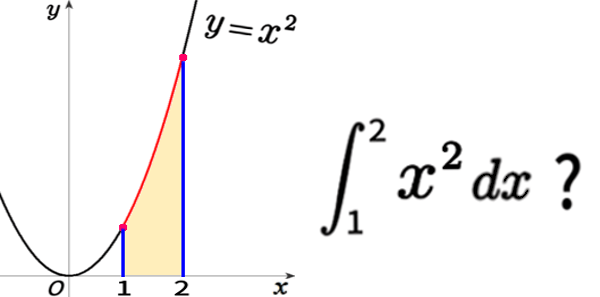
\(x^2\)の不定積分は?そうでしたね。
\(\displaystyle \int\, x^2 \,dx=\frac{x^3}{3} +C\) でした。
慣れたら「(\(C\) は積分定数)」は書かなくてもよいですが、
「\(+C\)」を書くことだけは 忘れないようにしましょう。不定積分としては。
今は定積分の計算ですが、その式を憶えておいて、いきなり代入して使います。
\(\displaystyle \int_1 \!\!\!\!\! \phantom{l^{\int}}^2 \, x^2 \,dx= \left[ \,\frac{x^3}{3} +C\, \right]_1 \!\!\!\!\!\! \phantom{l^{\int}}^2 \)
というように。
この先の計算は?…
「まで」の数を代入した値 -「から」の数を代入した値
をやるでしょう。
そのとき「\(+C\)」は!? たしてまたひくから、消えてどうせゼロになりますね。
そこで計算の工夫。
定積分の場合には、「\(+C\)」は初めから書かない
ようにするのです。それを分かったうえで、はじめから計算を書き直してみましょう。
\(\displaystyle \int_1 \!\!\!\!\! \phantom{l^{\int}}^2 \, x^2 \,dx= \left[ \,\frac{x^3}{3}\, \right]_1 \!\!\!\!\!\! \phantom{l^{\int}}^2 \)
続きは、代入・計算 …
\(\displaystyle \qquad\quad =\frac{2^3}{3}-\frac{1^3}{3}={\mathbf{\frac{\,7\,}{3}\,.}} \)
… 答えの数値が求まります。
不定積分 ⇒ 「\(+C\)」つける
定積分 ⇒ 「\(+C\)」は省略する
ということに注意です。
高校で習う微分の公式一覧
「微分の定義」、「微分の公式(抽象編)」 の「和, 差, 定数倍」、「微分の公式(具体編)」 の最初の項目 まで が 数Ⅱ。その他は 数Ⅲ。
- 微分の定義
- 微分の公式(抽象編)
- 微分の公式(具体編)
- 連続性の理論的考察、中間値の定理
- 微分可能性、平均値の定理
- 第2次導関数の性質:凸性
微分の定義
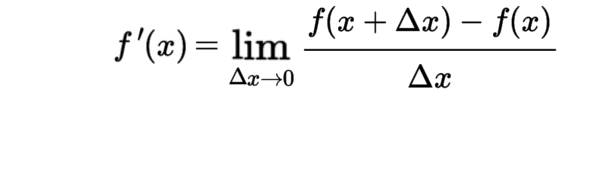
定義のし方から、\(f\,’(x)\) 以外にも \(\displaystyle \frac{dy}{dx}\)
という記号もある!
\(x\)が一つの決まった値\(a\) のときを微分係数、実数\(x\)を動かす使い方のときを導関数と呼ぶ。
この値が定義できるときを、「微分可能」と呼び、そうでないときを「微分不可能」と呼ぶ。微分可能性が問題になる場合は数三で。
以下の公式はすべて、微分の定義から証明される!
定義の意味「グラフの接線の傾き」ということから直ちに、
接線の方程式:\(y-f(a)=f\,’\,(a)\,(\,x-a\,)\) ,
法線の方程式:\(y-f(a)=-\dfrac{\,1\,}{f\,’\,(a)}\,(\,x-a\,)\)
ー と記せる。ただし分母になる値は\(\neq 0\ \ \)。
ここで述べておくと、
(ある範囲で定義された)導関数 \(f\,’\,(x)\) が

極大値または極小値を 極値 と総称する。
\(f\,’\,(x)=0\) となっただけでは極値になるとは限らない。前後で符号変化しない限りは。
これら性質を応用した、増減表をかくことで、グラフを描くことが可能になる。
微分の公式(抽象編)
微分可能な関数\(f(x),\,g(x)\)、\(a,\,b\) は実数のきまった数。
| 和, 差, 定数倍 | \(\{\,a\,f(x)+b\,g(x)\}\,’=a\,f’(x)+b\,g’(x)\) (\(b\)を負の数とすれば、引き算(差)について言えることに!) |
| 積 | \( \{ f(x)g(x) \}\,’=f\,’(x)g(x)+f(x)g\,’(x)\,. \) |
| 商 | さらに分母の関数\(g(x)\)の値はゼロにならない ものとして、 \(\displaystyle \left\{ \frac{f(x)}{g(x)} \right\} \,^{\displaystyle ’}=\frac{f’(x)g(x)-f(x)g’(x)}{\{ g(x) \} ^2 }\,. \) |
| 合成関数の微分 | \( u=f(x),\,y=g(u) \)つまり、 \(x\mapsto u\mapsto y\)で すべて 微分可能のとき \(\displaystyle \frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx} \) . |
| 逆関数の 微分 | \(y=f(x)\) が微分可能で \(f\,’\,(x)\neq 0\) 、 かつ逆関数 \(f^{-1}\,:\,y\mapsto x\) が存在するとき、 \(\dfrac{dx}{dy}=\dfrac{1}{\frac{dy}{dx}}\) . |
微分の公式(具体編)
- \( (x^{\alpha} )\,’=\alpha\,x^{\alpha -1} \) (\(\alpha\neq 0\) )
定数関数\(C\)の場合、\(C\,’=0\,.\) - \( (\sin x )\,’=\cos x ,\, (\cos x )\,’=-\sin x \)
- \( (\tan x )\,’=\displaystyle \frac{1}{\cos ^2 x} \)
- \( (e^x )\,’=e^x ,\, (a^x )\,’=a^x \log a \) (\(a>0\) )
- \( (\log x )\,’=\dfrac{1}{x} \) (底は自然対数の底\(e\) . )
- 対数微分法:関数 \( y=f(x) \) を微分するのに、
両辺の「log」(底は自然対数の底\(e\) )をとり
\( \log y =\log \{ f(x) \} \)
↓
それから微分する。
\( \{ \log y\}\,’ =\displaystyle \frac{y’}{y} \ \Longrightarrow\ y’\,= y\,\{ \log y\ \}’ \ . \)
連続性の理論的考察、中間値の定理
- 関数 \(f(x)\) が \(x=a\) で連続 とは、
\(\displaystyle \lim_{x\to a}\,f(x)\) が存在(両側極限 ! )して\(=f(a)\)
なること。
「微分法」の単元に含めて語られますが、連続性は本来、微分法からは独立した性質です。 - 【中間値の定理】
区間 \([\,a\,,\,b\,]\) で連続な関数 \(f(x)\) は、\(f(a)\) から \(f(b)\) の任意の値をとる。
このことを明確に表すには、\(f(a)\) と \(f(b)\) の値が 異符号 になるように設定し、0 となる値が少なくとも1つ存在する、という言い方をする。
微分可能性、平均値の定理
- 「微分の定義」の値が存在(両側極限 ! )するとき、微分可能であるという。
微分可能 \(\Longrightarrow\) 連続 である! - 【平均値の定理】
区間 \([\,a\,,\,b\,]\) で連続、\((\,a\,,\,b\,)\) で微分可能な関数 \(f(x)\) は、少なくとも1か所の\(c\) \((\,a<c<b\,)\) における微係数 \(f\,’\,(c)\) が、両端の平均変化率\(\dfrac{f(b)-f(a)}{b-a}\) と等しくなる。
← 両端の値が等しい場合の ロルの定理 から導かれる。ロルの定理は、最大値原理と呼ばれる大学で学ぶ知識からまた示されるので、高校では証明できなくてよい。
第2次導関数の性質:凸性
関数 \(f(x)\) を微分し、続けてもう1回微分した関数を、第2次導関数 \(f\,{}^{\prime\prime}\,(x)\) という。「エフ ツーダッシュ X」
例:\(f(x)=x^4\ \rightarrow\ 4x^3 \rightarrow\ 12x^2\,=f\,{}^{\prime\prime}\,(x)\)
$$\begin{cases} \text{ある範囲で }f\,^{\prime\prime}\,(x)>0\ \Longleftrightarrow\ 下に凸 \\ \text{ある範囲で }f\,{}^{\prime\prime}\,(x)<0\ \Longleftrightarrow\ 上に凸 \end{cases}$$
「下に凸」とは例えば、\(y=x^2\) の形状。任意の2点を線分で結ぶと、常にグラフが下側にある形状。
「上に凸」とは例えば、\(y=-x^2\) の形状。
思い浮かべるとよい。
\(f\,{}^{\prime\prime}\,(x)=0\) となり、前後で符号変化する場合、その点を 変曲点 という。
高校で習う積分の公式一覧
「具体的な公式1」の2項目め までが 数Ⅱ。以降は 数Ⅲ。
- 不定積分が、微分の逆。「\(+C\)」を忘れないこと。
- 定積分
- 定積分で例えば「\(\displaystyle \int_3 \!\!\!\!\! \phantom{l^{\int}}^2 \ \dotsm \)」
- 具体的な公式1
- 置換積分
- 部分積分
- 具体的な公式2
- 分数関数(有理関数)の積分のまとめ
不定積分が、微分の逆。「\(+C\)」を忘れないこと。
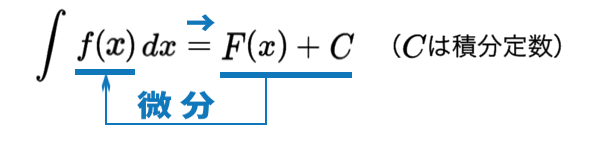
定積分
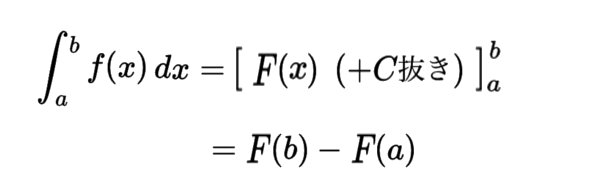
定積分で例えば「\(\displaystyle \int_3 \!\!\!\!\! \phantom{l^{\int}}^2 \ \dotsm \)」てのも可。
● \(\displaystyle \int_b \!\!\!\!\! \phantom{l^{\int}}^a \ \dotsm =-\int_a \!\!\!\!\! \phantom{l^{\int}}^b \ \dotsm \) ● \(\displaystyle \int_a \!\!\!\!\! \phantom{l^{\int}}^a \ \dotsm =0 \)
● \(\displaystyle \int_a \!\!\!\!\! \phantom{l^{\int}}^b \ \dotsm +\int_b \!\!\!\!\! \phantom{l^{\int}}^c \ \dotsm =\int_a \!\!\!\!\! \phantom{l^{\int}}^c \ \dotsm \)
(ただし各等式内の被積分関数は共通のこと。)
具体的な公式1
- \( \displaystyle \int\, x^{\alpha}\,dx = \frac{x^{\alpha +1}}{\alpha +1}+C \) ( \( \alpha\neq -1 \) の実数)
- 6ぶんの公式:
\(y=a\,x^2\) の形の放物線と直線が、\(x=\alpha\,,\,\beta\) の2点で交わるとき、間の囲まれる面積 \(S=\dfrac{|\,a\,|}{6}\,|\,\alpha -\beta\,|^3\) .
証明は、\(\displaystyle \int_{\alpha} \!\!\!\!\! \phantom{l^{\int}}^{\beta}\ a\,(\,x-\alpha\,)\,(\,x-\beta\,)\ dx\) の絶対値を計算すればよい。 - \( \displaystyle \int\, \sin x\,dx = -\cos x +C,\)
\(\displaystyle \int\, \cos x\,dx = \sin x +C \) - \( \displaystyle \int\, e^x\,dx = e^x +C\ ,\ \int\, a^x\,dx = \frac{a^x}{\log a} +C\) ( \( a>0 \) )
置換積分(積分テクニック1)
| おきかえ積分の場合 | \( f(x) \)を積分したいとき、その中の\( x \)の式の塊を\( u \)とおいたら、簡単になるときがある。\( f(x) \)を\( u \)の式で表したものを\( g(u) \)としたとき、 \( \displaystyle \int\,f(x)\,dx = \int\,g(u)\, \left( \frac{du}{dx} \right) ^{-1} du \) と、計算することができる。それが置換積分(おきかえ積分)! 定積分の場合、「から」の数と「まで」の数も、\( u \)の値域におきかえる。 ※ おきかえ積分の場合、\(x\)から\(u\)への関数は 1対1 でなければなりません。逆関数の微分が出てくるので。とくによく出てくるおきかえ積分は、1次式をかたまり\(u\)と考える場合で、暗算でできるよう公式にまとめておきます: \( \displaystyle \int\,f(ax+b)\,dx=\frac{\,1\,}{a}\,F(ax+b)+C \) (ここで \( \displaystyle \int\,f(u)\,du= F(u)+C \) ) |
| パラメータ積分の場合 | \( f(x) \)を積分したいとき、\(x\)がまた、他の変数\(t\)の関数になっているとき、 \( \displaystyle \int\,f(x)\,dx = \int\,f(x(t))\,\frac{dx}{dt}dt \) と、計算することができる。 「おきかえ積分」が\(x\)から他の文字への関数なのに対して、 この積分は、他の文字から\(x\)への関数。 どちらの積分も、「合成関数」になるので、変域には要注意。 この「パラメータ積分」の方は、高校では通常、定積分で使われる。 不定だと、大学で学ぶ「逆三角関数」で表す必要が出てくるため。 |
部分積分(積分テクニック2)
積分したい関数が例えば、\( e^x\,\sin x \)のように、関数の積(かけたもの)になっていて、かけられている要素(例えば\(e^x\)だけとか\(\sin x\)だけ) だけだったら積分できるのに… というときには、この積分テクニックが使われる。定積分の方で説明すると、
\( \displaystyle \int_a \!\!\!\!\! \phantom{l^{\int}}^b \,f(x)\,g(x)\,dx = \int_a \!\!\!\!\! \phantom{l^{\int}}^b \,\{ F(x) \}\,’\,g(x)\,dx\)
\( \displaystyle =[\, F(x)\,g(x)\,]_a \!\!\!\!\!\! \phantom{l^{\int}}^b \mathbf{-} \int_a \!\!\!\!\! \phantom{l^{\int}}^b \,F(x) \,g\,’\,(x)\,dx\)
\(f(x)\)の方を上げる(積分する)方で表したが、\(g(x)\)の方でも同様。
具体的な公式2~積分テクニック1,2によって得られるもの
- \( \displaystyle \int\, \frac{f\,’\,(x)}{f(x)}\,dx=\log |f(x)|+C \)
例えば \( \displaystyle \int\,\tan x\,dx= -\log |\tan x| +C \) 、
\( \displaystyle \int\,\frac{dx}{x}=\log |x| +C \) . - \( \displaystyle \int\, \{ f(x)\} ^{\alpha} f\,’\,(x)\,dx=\frac{\{ f(x) \} ^{\alpha +1} }{\alpha +1}+C \)
( ただし \( \alpha\neq -1 \) ) - \( \displaystyle \int\,\log x\,dx = x\,\log x-x+C \)
- \( \displaystyle \int_a \!\!\!\!\!\! \phantom{l^{\int}}^b \,f(A^2 -x^2 )\,dx\) → \( x=A\sin\theta \)とおく
( ただし\(A>0\)、\(|a|\,,\,|b|\leqq A\) 。) - \( \displaystyle \int_a \!\!\!\!\!\! \phantom{l^{\int}}^b \,f(A^2 +x^2 )\,dx\) → \( x=A\tan\theta \)とおく
分数関数(有理関数)の積分のまとめ
一般の分数関数を積分するとき、まず分子を分母で割り、余りを出す。
\(\displaystyle \frac{A(x)}{B(x)}=\frac{B(x)Q(x)+R(x)}{B(x)}=Q(x)+\frac{R(x)}{B(x)} \)
↓
次に、そうして残った分数の部分の、分母を実数の範囲で因数分解。
そして、R/B 部分について一般的な部分分数分解:
\(\dfrac{\phantom{mmm}P(x)\phantom{mmmm}}{(x-\alpha )^m (\text{虚数解の2次式})}\)
\(\ \ =\dfrac{a_1}{x-\alpha}+\dotsm +\dfrac{a_m}{(x-\alpha )^m}+\tfrac{\displaystyle bx+c}{(\text{虚数解の2次式})}\)
係数は、通分して、係数比較で求める。
↓
各項を別々に積分すればよい。ただし
\(\displaystyle \int\,\frac{1}{\scriptsize{(\text{虚数解の2次式})}}\,dx = \int\,\frac{1}{(x+\beta )^2 +R^2 }\,dx \)
平方完成した
\(\displaystyle \int\,\frac{1}{(x+\beta )^2 +R^2 }\,dx=\frac{\,1\,}{R}\text{Arctan}\,\frac{x+\beta}{R}+C \)
身の回りにある 微分積分を使った事例
「積分は面積」と言ってきたのですが、最初の方の例題:
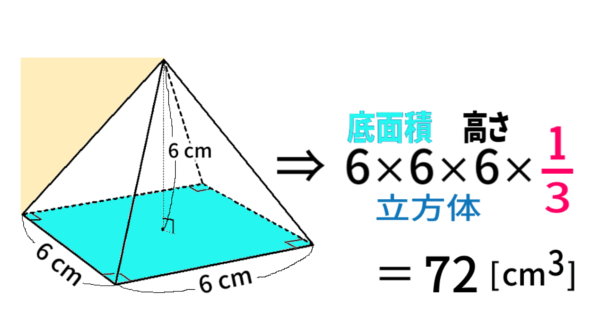
のように、体積の計算にだって応用できるのです。
なぜ「 \(\dfrac{\,1\,}{3}\) 」をかけるのか?
積分を使って、解答してみましょう。
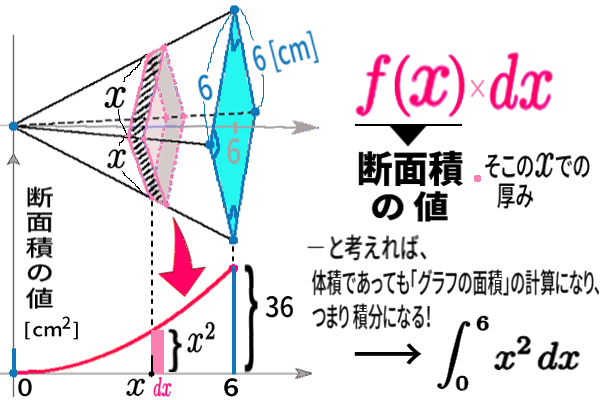
前に、積分とは「グラフの面積の『計算方法』」と言ったのはこのためです。すなわち、\(x\)における断面積の値を関数・グラフとすることで、体積を求めるために「グラフの面積」を計算すればよいからなのです。
計算を最後の近くまでやっておきましょう。
\(\displaystyle \int_0 \!\!\!\!\! \phantom{l^{\int}}^{6}\, x^2 \,dx = \left[ \,\frac{x^3}{3} \,\right]_0 \!\!\!\!\!\! \phantom{l^{\int}}^{6} \)
\( =\displaystyle \frac{\,1\,}{3}\times 6^3 \)
だから、\( \displaystyle \frac{\,1\,}{3} \)をかけることになるのです。
計算を最後まで行うと、答えは72 [\(\text{cm} ^3 \)]となります。
問題編
まずは、微分の公式を、計算で導いて(証明して)みましょう。
[例題1] \((\,x^2\,)\,’\,=2x\) を証明しなさい。
[解] 微分の定義を使います。
\(\displaystyle \lim_{\Delta x\to 0}\,\frac{(\,x+\Delta x\,)^2 -\,x^2}{\Delta x}\)

\(\Delta x\) はゼロに近づく数ですが、ゼロと等しくはしない数。だから割れます。lim の式は最後に、ゼロに等しくなっても構わない つまり、代入できるようになった場合(本当はゼロの所で連続性が成り立つから)には初めて、代入して答えてよくなります!

