行列、行列式の意味と定義、計算法もわかりやすく解説【線形代数】

行列、行列式とは何かというと

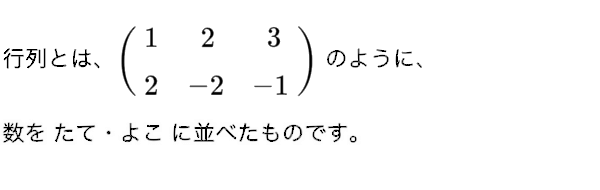
その始まりは、
連立方程式（１次連立方程式）の係数だけ集めて、注目したことがきっかけです。

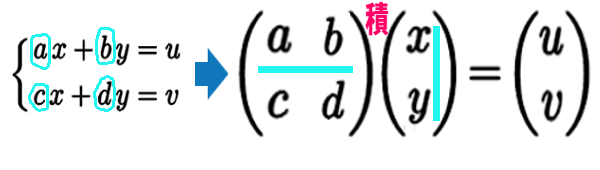
２個の行列が続いているのは

掛け算 ( 積演算 ) の意味。
左側の行列は横に切り、右側の行列は たてに読んで、かけて足す 計算です。

数が１列（または１行）だけの行列とはベクトルです。
ベクトルでやるように、行列で
定数倍　$k\,\text{A}$ と言ったら、

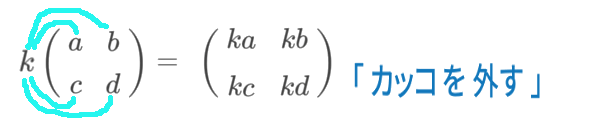
　のように、計算するもののことです。
行列を一文字でおくときは、通常大文字 A, B,$\dotsm$ を使います。

(１次)連立方程式の解を求めるとき、最後割らなければならない値 のことです。

２元連立方程式(係数は一般に $a\,,\,b\,,\,c\,,\,d$)
の場合

次の２元 (１次 ) 連立方程式を解いてみます。

$$\ \begin{cases} \,ax+by=u \\ \,cx+dy=v \end{cases}$$

いわゆる加減法(消去法) 。片方の文字の係数を揃えて、引き算…

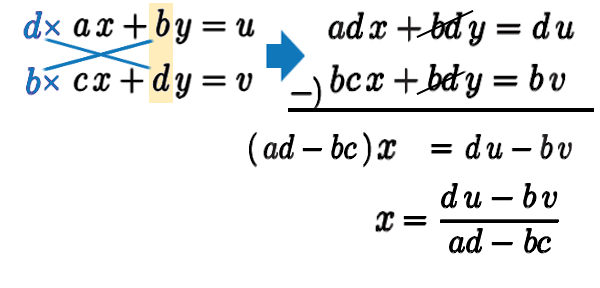
片方の文字解 $x$ が求まったらいつもは、代入しに行くのですが、今は係数がすべて文字。
計算が面倒という理由で、また最初の式に戻り、加減法で今度は $x$ を消し、解を求めます。

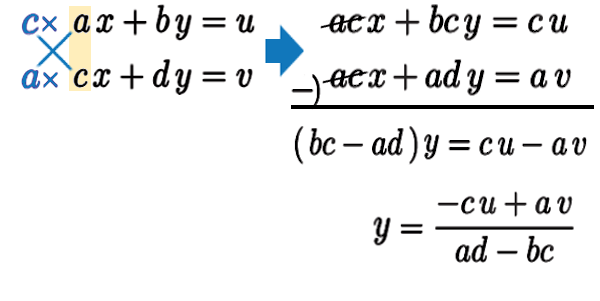
$x$ の分母に $y$ も合わせるよう、異符号すなわち、分母分子に $-1$ をかけます。
行列式とは、この分母、割る数。$ad-bc$ のこと。
解は $(\,x\,,\,y\,)=\left( \dfrac{d\,u-b\,v}{ad-bc}\,,\,\dfrac{-c\,u+a\,v}{ad-bc}\, \right)$ .
$x\,,y$ をたてに書き、定数項 $u\,,v$ については１次式ですから、行列の書き方で、

と書くことができます。
この分母割っている数、行列式。

の記号で表します。
これら記号の値が $=ad-bc$ になるということです。
しかし、

行列式の値がもしゼロだったら、連立方程式の解はどうなるか？

その場合、上のように解を計算することはできず、
連立方程式は解をもたないか、無数に解をもつかの
どちらかになります。

実際、$ad-bc=0$ ということは、

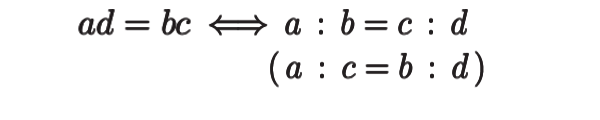
つまり、「比がそろっている」状態を意味します。
例えば、

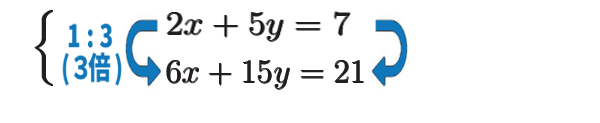
「比がそろっている」ので、正味
$\ 2x+5y=7$ の式１個だけが条件ということです。
これですと、$x$ を任意の値に決めて、$y$ の１次方程式を解けば $y$ の値が決まり、そうした値はすべて条件を満たすわけだから、すべてこの連立方程式の解。解は無数にあることになります。
図の意味で言うと、直線を表し、直線上のすべての点が解、ということです。

また例えば、

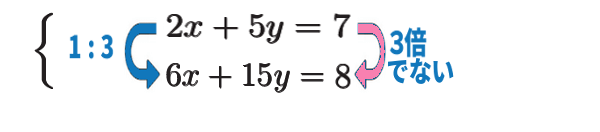
左辺の比はそろっていて、左辺の値全体が３倍です。しかし右辺の値は３倍でないようになっている、それは根本的に矛盾した条件。
どんな $x\,,\,y$ の値をもってしても満たすことはできず、したがって解なしです。
図の意味では、平行な２直線。交わった所が解なのですが、これでは永久に交わることがありません。

まとめると次のようです：
連立方程式 $\begin{pmatrix} a&b \\ c&d \end{pmatrix}\,\begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} u \\ v \end{pmatrix} $ で

行列式 $\Delta\,(=ad-bc)\,\neq\,0$	解はただ１組
行列式 $\Delta\,=\,0$　かつ　　　　左辺の比$=$右辺の比	解は無数 ( 不定の解 )
行列式 $\Delta\,=\,0$　かつ　　　　左辺の比$\neq$右辺の比	解なし ( 不能の解 )

３次元の場合、行列式は？連立の解は？

これまでは、２元連立方程式、行列はたてに数が２個、よこにも２個の、２×２(正方) 行列を扱ってきました。
２次元とも呼ばれます。
それでは文字がもう１個増えた、３元連立方程式では、
どうでしょうか？。３次元です。

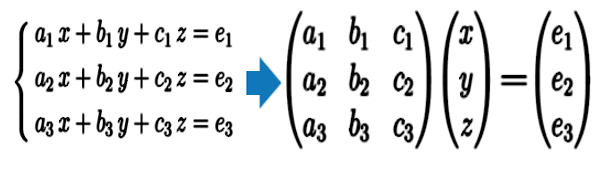
係数を表すのに $c$ 以降 $d\,,\,e\,,\dotsm$ では文字が足りなくなるので、添字を使って表し始めます。

行列は３×３(正方)行列です。行列式はどうなるでしょうか？。
３元連立方程式を解く解き方をやってみれば、求められます。
中学の応用問題で出てきた解き方を思い出してみましょう。

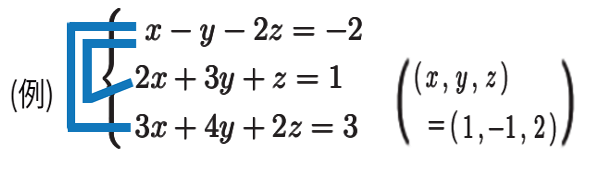
式と式を比べて、$x\,,\,y\,,\,z$ のうち一文字を完全に消去し、よく分かる２元連立方程式に帰着させて、解くのでした。
この解法にならって、文字係数のまま解いてみましょう。

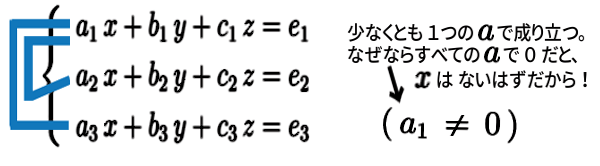
他の２つの式のいずれとも比べるための１つめの式は、$a_1\,\neq\,0$ としておきます。
係数そろえて完全に消去したい文字は $x$ とします。

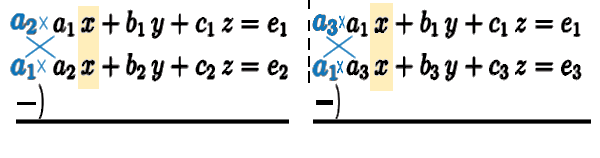
「 $a_1$ 」をかけた方が先に来るように、式全体にマイナスをかけて、

係数は先ほど出てきた、２×２の行列式です。
結局、$y$ と $z$ は２元連立方程式

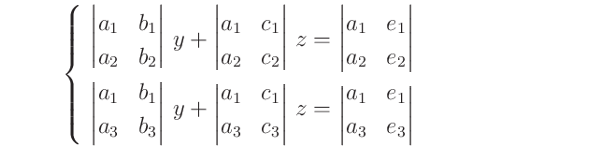
になります。先ほどの２元連立方程式の解の公式で、
解 $y\,,\,z$ は表すことができます。

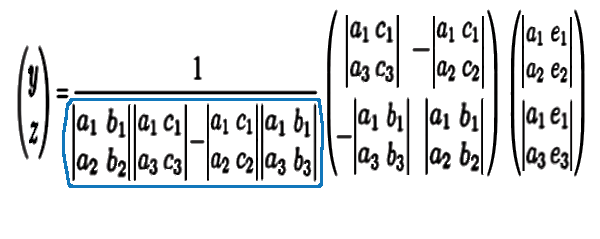
解の計算の最後に、この青で囲んだ値で割るのですが。

割る数だからこれが行列式か

とも思えますが、まだ分かりません。
今回は３元。３×３行列。より複雑です。計算を進めてみます。

「置換」が登場。符号、奇置換、偶置換 …

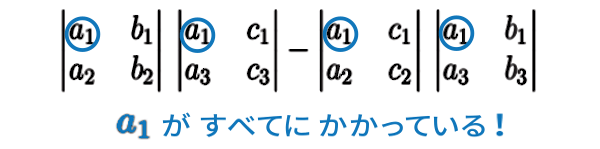
$ \ =(a_1\,b_2-a_2\,b_1)\,(a_1\,c_3-a_3\,c_1)$
$ \qquad\qquad -(a_1\,b_3-a_3\,b_1)\,(a_1\,c_2-a_2\,c_1)$

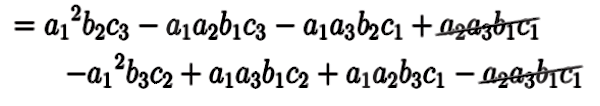
$a_1$ がすべてにかかっているので、$a_1$ でくくってみると、

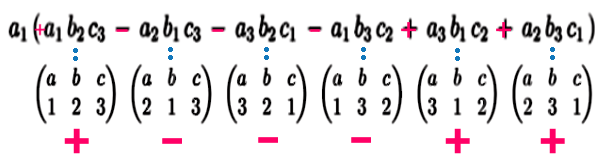
カッコの中に注意すると、項が６個あります。
そして、$a\,,\,b\,,\,c$ について番号1, 2, 3 のすべての並べ方が現れています。確かに
$3\,!=6$通りです。これら番号の並べ方を、

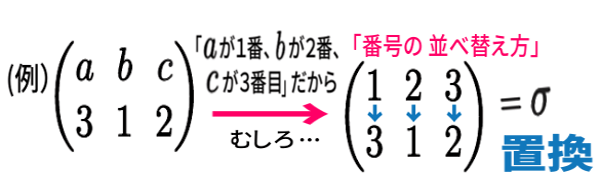
と表しましょう。青の矢印は元々書きませんが、そのように番号が対応する という意味です。
記号を使うと（よくシグマ( $\sigma $ )を使います）この例は、
$ \sigma(1)=3\,,\,\sigma(2)=1\,,\,\sigma(3)=2$ のように関数で言い表せて、置換と呼ばれます。
形は行列みたいですが、行列とは意味が異なります。

次に、(再掲)

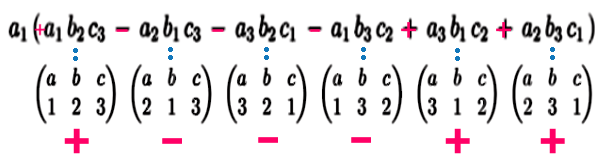
プラスになったりマイナスになったり、不思議なので
赤で書いておいたのですが、
この符号はどうやって変わるのかについて、見ていきましょう。(やはり「 $ a\,,\,b\,,\,c$ 」よりも「 1, 2, 3」( 番号 )で本当は見るべきです。)
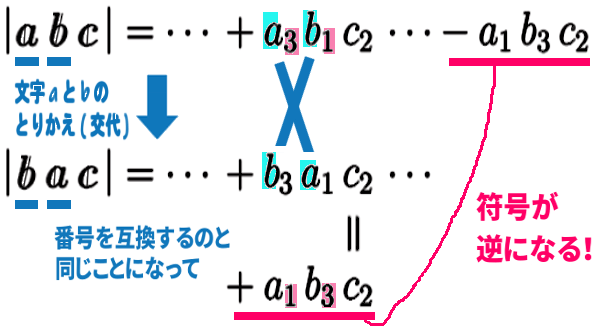
上のカッコ内の６項のうち次の２項を例えば比べると、

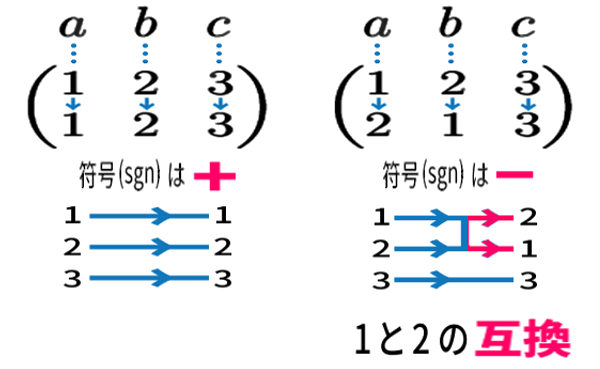
２つの番号だけ並べ替える ( 互換と呼びます )と、符号が変わると分かります。
互換のイメージは、あみだくじの 横断する線 ( この図では たての線。通常と異なりこの図では、あみだくじを横向きに描いています ) です。
次にまた互換を行う、つまり２回目の互換を行うと、また符号が変わるから、最初の符号。プラスに戻ります。
実は置換(並べ替え) はすべて、そうやって 互換を繰り返し行って得られるもので、符号はその度に反転する、ということなのです。
置換には $3!=6$通りありました。そのすべて。互換０回から数え始めます。

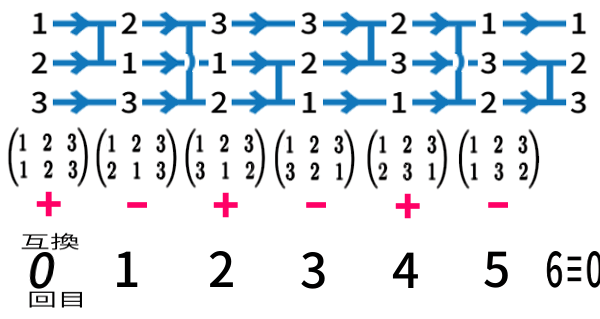
初め $\begin{pmatrix} 1&2&3 \\ 1&2&3 \end{pmatrix}$ 。まったく入れ換えてない状態から、互換を１回、３回、５回行なってできた置換は、奇数回マイナスをかけた「マイナスの」置換で、奇置換と呼ばれます。
その反対に、互換を０回、２回、… 偶数回マイナスをかけた「プラスの」置換。偶置換と呼ばれます。
このプラス／マイナスを、その置換 $\sigma$ の符号と呼び、$\text{sgn}\,(\sigma )$ と書くことがあります。
それぞれの置換を見てその符号がどちらになるかは、瞬時に判定できなくて構いません。

それでは、３×３行列の行列式とは？

結局、解 $y\,,\,z$ を求めようとして、分母つまり割る数となる

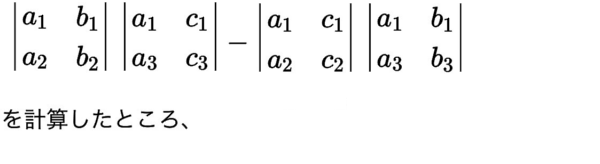
$ = a_1\,(\ a_1\,b_2\,c_3-a_2\,b_1\,c_3+a_3\,b_1\,c_2$
$ \qquad -a_3\,b_2\,c_1+a_2\,b_3\,c_1-a_1\,b_3\,c_2\ ) $
となります。$a_1 $ でくくれるのでした。
カッコの中は、置換の考え方で見ると見やすくなる形の式ですね。
一方、解例えば $y$ の方は、

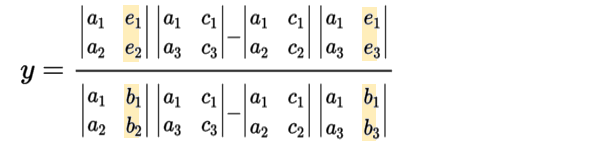
複雑ですが、よく見ると、分母の $b$ が $e$ に置き換わったものが、分子です。だから、計算した後の式も、分母の $b$ を $e$ に置き換えて

そうすると $a_1$ で約分することができるので、解 $y$ の式が簡単になって、

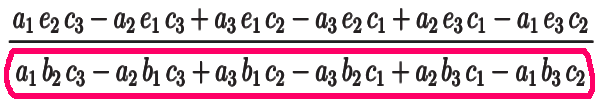
これが真に割る数。行列式だと、確定できたことになります。
したがって次のように定義します：

右辺は$a\,,b\,,c$、1, 2, 3 について対称性があって、３×３行列についての式だといえます。
すべての置換をわたる、符号をつけた各項の和、とも言い表せます。
det や $\Delta\,,\,\delta$ という記号も使えます。

３×３つまり３次元の行列式となると、だいぶ複雑で、工夫なしに覚えるのは困難です。
( 後でまとめますので、ここまではノートも取らなくて大丈夫です。)

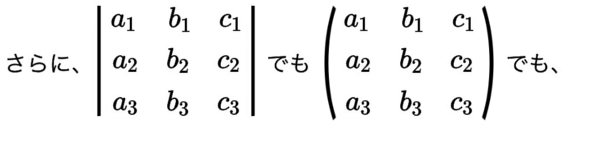
たて一列々々、ベクトルのかたまりとして考え、

３×３行列の行列式もゼロになる場合はあります。しかし暫くは $\neq 0$ であるとして、３元連立の解の公式の導出を続けましょう。
３×３の行列式で表せば、解$y\,,\,z$の式は簡潔になります。

$y=\dfrac{|\,\mathbf{a}\,\mathbf{e}\,\mathbf{c}\,|}{|\,\mathbf{a}\,\mathbf{b}\,\mathbf{c}\,|}\ ,\ z=\dfrac{|\,\mathbf{a}\,\mathbf{b}\,\mathbf{e}\,|}{|\,\mathbf{a}\,\mathbf{b}\,\mathbf{c}\,|}\ .$
先ほど、$y$の分子は $b$ を $e$ でおきかえればよいと、
同様に $z$の分子は、$c$ を $e$ でおきかえたものだと、分かっていたので、そうなります。

そして３元連立の解。残り、$x$ も求めなければなりません。
何となく、$y$の分子が $b$ を $e$ で、$z$の分子が $c$ を $e$ でおきかえたものだから、$x$の分子は $a$ を $e$ でおきかえたもので、
$x=\dfrac{|\,\mathbf{e}\,\mathbf{b}\,\mathbf{c}\,|}{|\,\mathbf{a}\,\mathbf{b}\,\mathbf{c}\,|} $ ではないかと予想されます。
実はそれで正しいのですが、それを確かめるためにまず、

行列式の性質　交代性について

みていきましょう。
交代性とは、行列のたて１列と他のたて１列を並べ替えると、その行列式の値はマイナスがかかった異符号になる、という性質です。(横１列(１行) どうしでも成り立ちます。)

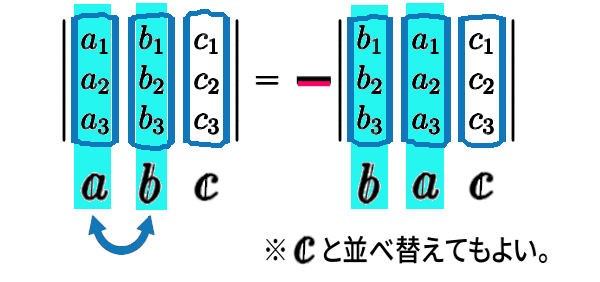
なぜそのような性質が成り立つかというと、行列の１列と他の１列を並べ替える操作は、行列式の各項に一斉に互換を施す意味と、同じことになるからです。

それでは３元連立の残りの解 $x$ を。

$y\,,\,z$ が分かっているから代入する、という方法ではかえって計算が大変になるので、最初から解き直してみます。
$x$ を消去する代わりに今度は、 $y$ を消去します。見やすくするため、$y$ の項を最も左に配置します。

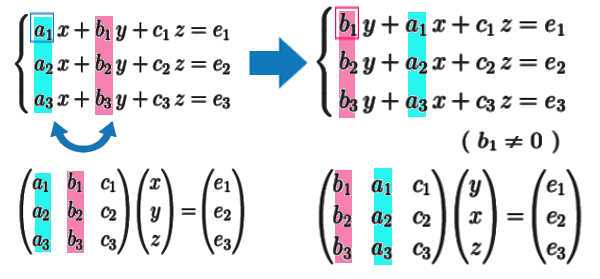
係数も左の２列が並べ替わります。最初３元連立を解いたとき $a_1$ を他の式のそれぞれの係数にかけて $x$ を消去したように、今度は $b_1$ を他の式のそれぞれの係数にかけて $y$ を消去していきます。

そこでは $b_1\neq 0$ を仮定しなければなりません。もし最初の第１式 $b_1 y+a_1 x+c_1 z=0$ の $b_1$ が０だったら、他の、$b_k\neq 0$ を満たす第k式を代わりに第１式に上げなければならず、その場合はさらに行列の行と行の並べ替えを行う必要があるでしょう。

しかしそうした操作を行なったとしても、
係数の行列式は、初めの行列式 $ \begin{vmatrix} a_1&b_1&c_1 \\ \ a_2&b_2&c_2 \\ \ a_3&b_3&c_3 \end{vmatrix} $ に
$\pm 1$をかけたものにしか、せいぜいなりません。

あとは最初の解き方としくみはまったく同じなので、
最初の解き方で出た解の公式を、$a$ を $b$ , $b$ を $a$ ,
$x$ を $y$ , $y$ を $x$ に読み替えれば、今得られる解のはずです。

$x=\dfrac{|\,\mathbf{b}\,\mathbf{e}\,\mathbf{c}\,|}{|\,\mathbf{b}\,\mathbf{a}\,\mathbf{c}\,|}\ \ ,\ \ z=\dfrac{|\,\mathbf{b}\,\mathbf{a}\,\mathbf{e}\,|}{|\,\mathbf{b}\,\mathbf{a}\,\mathbf{c}\,|}\ \ \ .$

これに交代性を使います。初めは $z$ から。

$ z=\dfrac{|\,\mathbf{b}\,\mathbf{a}\,\mathbf{e}\,|}{|\,\mathbf{b}\,\mathbf{a}\,\mathbf{c}\,|}=\dfrac{-|\,\mathbf{a}\,\mathbf{b}\,\mathbf{e}\,|}{-|\,\mathbf{a}\,\mathbf{b}\,\mathbf{c}\,|} $
　　$ =\dfrac{|\,\mathbf{a}\,\mathbf{b}\,\mathbf{e}\,|}{|\,\mathbf{a}\,\mathbf{b}\,\mathbf{c}\,|} $
となり、最初出した答えと一致すると確認できました。
ではいよいよ $x$ です。とはいえ今の計算とまったく同様で難しくありません。

$ x=\dfrac{|\,\mathbf{b}\,\mathbf{e}\,\mathbf{c}\,|}{|\,\mathbf{b}\,\mathbf{a}\,\mathbf{c}\,|}=\dfrac{-|\,\mathbf{e}\,\mathbf{b}\,\mathbf{c}\,|}{-|\,\mathbf{a}\,\mathbf{b}\,\mathbf{c}\,|} $
　　$ =\dfrac{|\,\mathbf{e}\,\mathbf{b}\,\mathbf{c}\,|}{|\,\mathbf{a}\,\mathbf{b}\,\mathbf{c}\,|}\ . $

これで、３元連立方程式の解の公式が、得られました。
$ x=\dfrac{|\,\mathbf{e}\,\mathbf{b}\,\mathbf{c}\,|}{|\,\mathbf{a}\,\mathbf{b}\,\mathbf{c}\,|}\,,\,y=\dfrac{|\,\mathbf{a}\,\mathbf{e}\,\mathbf{c}\,|}{|\,\mathbf{a}\,\mathbf{b}\,\mathbf{c}\,|}\,,\,z=\dfrac{|\,\mathbf{a}\,\mathbf{b}\,\mathbf{e}\,|}{|\,\mathbf{a}\,\mathbf{b}\,\mathbf{c}\,|}\ . $
( $ |\,\mathbf{a}\ \mathbf{b}\ \mathbf{c}\,| $ は、３次正方行列の行列式($\neq 0$) 。)

では次元を一般の $n$ 次元にして、$n$ 元一次連立方程式だったら⁉ー
それを考えるためには、a , b , c ,$\dotsm$ とやっていくと文字が足りなくなりますので、a , b , c ,$\dotsm$ の代わりに $\mathbf{a}_1\,,\,\mathbf{a}_2\,,\,\mathbf{a}_3\,,\,\dotsm$ と言っていくことにします。
すると行列の各要素 (成分) の添字は、縦も横も番号を使うことになるから、
「 $a_{2\,\!3}$ 」のような、二重添字になります。
二重添字の言い方で、これまで得られた公式を以下に、まとめます：

まとめ：行列とは？２元・３元の行列式の定義、性質と計算法

行列
行列とは、たて・横に、数を並べたもの。たてと横の個数が同じ場合 正方行列 と呼ばれます。
「行列」の名の通り、「行」,「列」の順に成分の位置を表します。

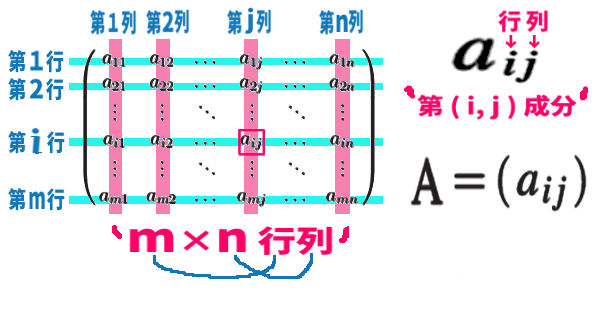
行列の演算 (定数倍・和差)
　$ \text{A}=(\,a_{ij}\,)\,,\,\text{B}=(\,b_{ij}\,)$ について、
　　$\alpha\text{A}+\beta\,\text{B}\,:=(\,\alpha\,a_{ij}+\beta\,b_{ij}\,)$ .
　AとBの演算では、AとBの行列のサイズが等しくなければなりません。
　要するに、各成分について演算します。
　
行列の演算 (積)
$ \text{A}=(\,a_{ij}\,)\,,\,\text{B}=(\,b_{ij}\,)$ について、
　A, B で表せば $\text{A}\,\text{B}$ という、掛け算 (積演算) 。
具体的な計算は以下のようですが、計算が定義できるためには必ず、
　Aの列の数 (横の個数) と、Bの行の数 (たての個数)が、等しい。
一致していなければなりません。

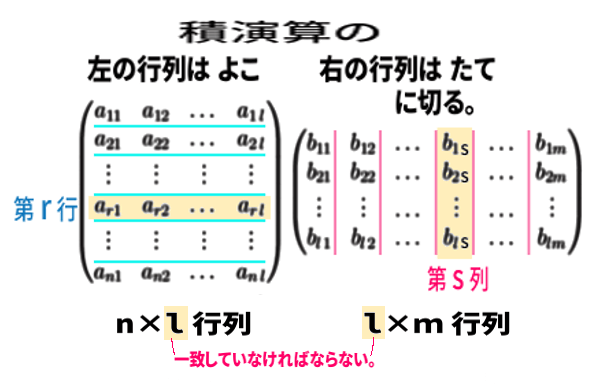
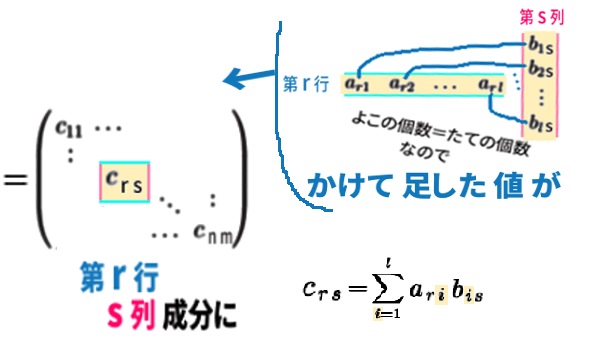
　　演算の結果の行列 C は、$n\times m$ 行列になります。

２元( ２×２行列 )の行列式
「 $a_{ij}$ 」(二重添字) の表記でやはり見ます。

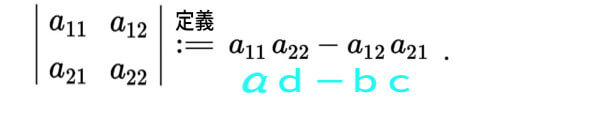
３元( ３×３行列 )の行列式の定義
先ほどは具体的にも書き出しましたが、次の定義をもとにしましょう。

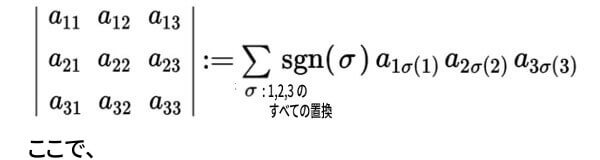
置換
３元( ３×３行列 )の行列式の計算法
具体的に書き出した式のほうでは、
次のように把握すれば憶えられます。
【関-サラスの計算法】:
行列のベクトル記法について
行列式の性質
(1) 交代性
(2) 多重線形性

行列、行列式の意味と定義、計算法もわかりやすく解説【線形代数】

行列、行列式とは何かというと