平方完成(２次関数)は これで必ずできる！くくって完全平方式を取り出すだけ。

[ 数Ⅰ ] 「２次関数」で学習する、

2次関数の式を
「グラフの描きやすい」形の式（標準形と呼ばれる）に直すための計算。

それが、平方完成です。

上位 ２項だけくくり
　　　↓
(カッコの中から) 完全平方式を取り出す
ー という、たった ツーステップ 2つの手順 で できます。

この計算を乗り超えるかどうかが、この後の「２次関数」そして数 ⅠA に 自信が持てるかどうかを決めると言っても過言ではない所です。

攻略するとしましょう。

まず、上位２項だけくくる。係数で。

「くくる」【括る】 というのは、よく出てくる言葉です。
確認しておきましょう。

それは カッコでまとめる という意味です。

例えば　 \( 2x^2 +4x\,=\,2\,(x^2 +2x)\)　の 左辺→右辺
のような。

そして、「上位２項」とは …
式 (きちんと言うと、整式 とか 多項式) では、
次数が上の・高い 項の順つまり、降べきの順 に注目される、ということがあります。

そこで降べきの順に見たとき、

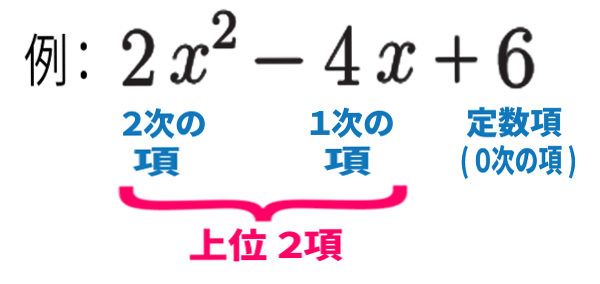
これらのことを指します。

ここで扱う式は、２次式。
２次, １次, 定数項(０次) の ３つの項があり、
そのうち、上位２項だけをくくるのです。

$$\Large{2x^2-4x+6=2\,(x^2-2x)+6}$$

というように。
\(2x^2-4x+6=2\,(x^2-2x+3)\)　というふうには しない ようにします。

係数で。正確には「２次の係数で」くくっています。
「係数」とは

… 項の中の「かけられている数」の部分のことでした。
だから計算は可能でも、
\(2x^2-4x+6=2x\,(x-2)+6\)　とはしません。

２次の係数で、上位の２項だけ、くくる

ー １つ練習してみましょう。どんな数値でも対応できるよう、数値は少し難しくしました。
[ 問１ ] 　\( -\dfrac{\,2\,}{3\,}x^2+3x+1 \) ?

こうやります。

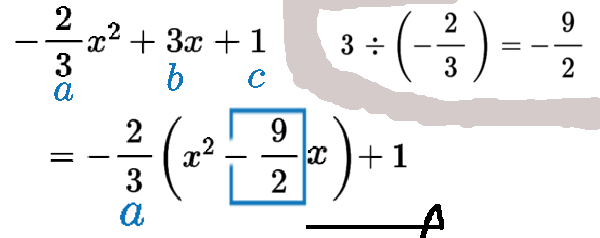
式のすぐ分かる所だけ先に
　　\(=-\dfrac{\,2\,}{3}\, \left( \,x^2 +\Box\,x \, \right)+1 \)
と考えておき、横の余白で計算する手順です。
\(\Box\) が、カッコを外したとき
　\(-\dfrac{\,2\,}{3}\times\Box=3\)　だから、かける の逆、割って、\(\Box\) を求める、
計算は横の余白で筆算し、出た答えを記入します。

符号は、初めに決めてしまっても良いでしょう。

係数 \(a\,,\,b\,,\,c\) で表して、今の手順をまとめますと、

２次の係数で、上位の２項だけ、くくる：

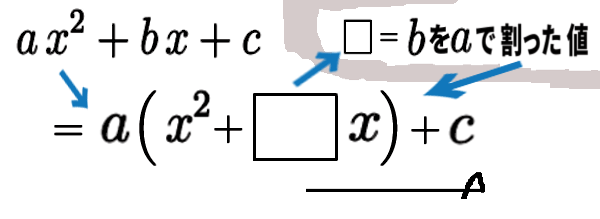
ただし２次式なので、\(a\neq\,0\) です。

次、カッコの中から完全平方式を取り出す

次いで、先ほど くくった、カッコの中身について計算を進めていきます。
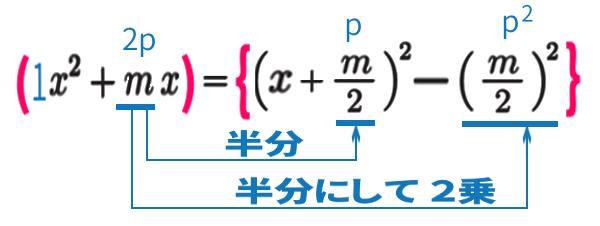
この 公式を使用します：

赤いカッコが、くくって できた カッコです。
覚える場合は、つけたまま覚えるようにしてください。

例えば、
\((\,\,x^2-6x\,)=\{\,\,(x-3)^2 -9\,\,\}\)　というように。
「6」は偶数なので 計算しやすいですが、たとえ奇数や分数の場合でも、同じように計算できなければいけません。

「半分」、「半分にして２乗」と
覚えましょう。「半分」とはすなわち、
「かける２分の１」です。

慣れてきたら、今の例のように カッコの外に何もない場合は、外側のカッコや中カッコは、省略してよいでしょう。

この公式は、どうやって導かれるか？
実は、中学の時、こういうことをやったと思います。

「\(x^2 -6x+\Box = (x-\Box\,)^2\) の □ をうめなさい。
　ただし２つの □は 同じ数ではない。」

右辺のような カッコの２乗の形の式は 完全平方(式) と呼ばれるのでした。
中３の 乗法公式 の１つにも出てきました。
\((a+b)^2 =a^2 +2ab+b^2 \)　、文字を変えて見ると

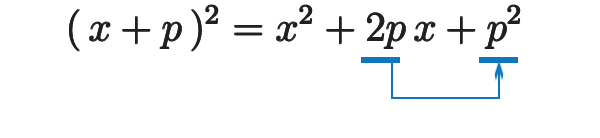
「 \(2p\) 」をもとにして、\(2p\mapsto p\mapsto p^2\) 。これって

「半分にして ２乗」ではないですか？　これで

「\(x^2 -6x+\Box = (x-\Box\,)^2\) 」にも解答できます。
９,３ と。

この完全平方式、左右辺 逆さにして、見ます。
その式をもとに、移項してみます。
ちなみに、等式であれば 何でもいつでも、移項 というものは、できます。
すると、

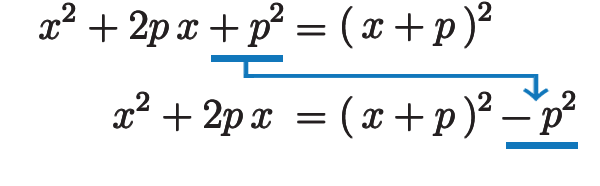
そこで、\(2p=m\) とおいたら。今の公式になっていないですか？。

再掲しましょう。

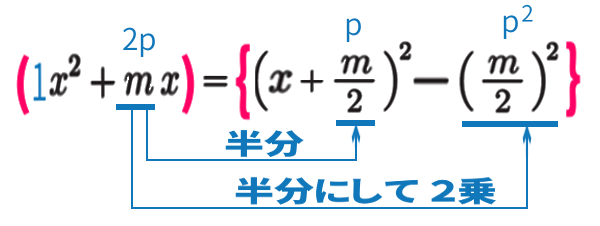
公式の正当性が分かったので、公式を使って、[ 問１ ] で出した計算の続きをやってみましょう。
[ 問２ ] \( \left( \,\,x^2 -\dfrac{\,9\,}{2}\,x\,\, \right) \) の計算の続きをしなさい。

[ 解 ] あえてカッコをつけておきました。

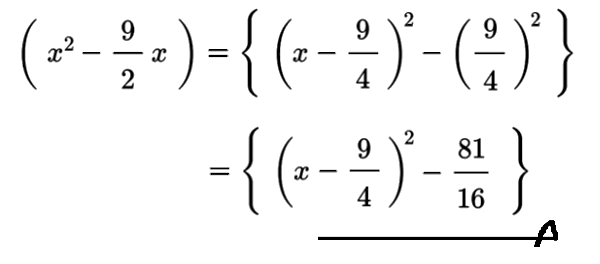
完全平方式が出てきて、残った部分が差になっている、
完全平方式を取り出す公式 と言えますね。
もちろん、\(m\,(\,=\,2p\,)\) が負の数であれば、\((\,x\,-\,\dotsm\,)^2\) となります。

最後に、中カッコ だけ 外すこと

[ 問１ ], [ 問２ ] 通しで計算すると、結局、

\( -\dfrac{\,2\,}{3\,}x^2+3x+1\,=\, -\dfrac{\,2\,}{3\,} \left( \,x^2-\dfrac{\,9\,}{2}\,x\, \right) +1\)
　　　　　\(=\,-\dfrac{\,2\,}{3\,} \left\{ \,\left( \,x-\dfrac{\,9\,}{4}\, \right) ^2-\dfrac{81}{16}\, \right\}+1\)

ー という式にまで到達します。

これで平方完成完了と言いたいところですが、最後の詰め を１点だけ。(２ステップに含みませんでしたが。)

最後に 中カッコ { … } だけ 外してください。

内側のカッコはそのままです。
上の式は 以下のように、最後まで計算し、

　　\(=\,-\dfrac{\,2\,}{3}\,\left( \,x-\dfrac{\,9\,}{4}\, \right) ^2 +\dfrac{\,2\,}{3}\times\dfrac{81}{16}+1\)
　　\(=\,-\dfrac{\,2\,}{3}\,\left( \,x-\dfrac{\,9\,}{4}\, \right) ^2 +\dfrac{35}{8}\) .
　ー まで行なって、完了です。

平方完成の まとめ

まとめると、２ステップ (または 2.5ステップ ) です。

• 係数で、上位の２項だけ、くくる
• カッコの中で、完全平方を取り出す公式を使う
• 最後、中カッコだけ、外す

もう１問、通しで、やってみましょう。数値は .. 複雑です。

[ 章末問題 ]　 \(y=\,-\dfrac{\,2\,}{5}\,x-3x+1\) の 平方完成 ？
[ 解 ]

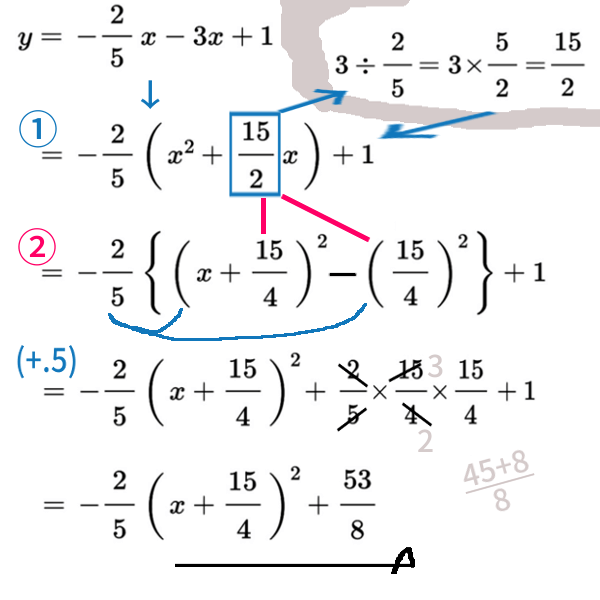
① 上位２項でくくり (必要な計算は横で) → ② 完全平方を取り出す公式で (「半分」、「半分にして ２乗」です。) → (+.5) 中カッコ{…} だけ、外すー必要な途中計算は周りで行なってよいー
この手順で、複雑な数でも成し遂げられました。

注意点。上位２項とは言っても …

あくまでも、２次の項と１次の項 のことです。

例えば \(-\dfrac{\,2\,}{3}\,x^2+2\) 　だったら。
「上位２項」と言っても \(=\,-\dfrac{\,2\,}{3}\,(\,x^2-3\,)\) とはせず、
\(-\dfrac{\,2\,}{3}\,x^2+2\) のまま。既にくくれてる、と考えます。

１次の項は、ない場合も「 \(0\,x\) がある」と考えてください。

平方完成は、何の役に立つの？

• ２次関数の標準形。頂点が分かる形にすること
• ２次方程式の解の公式

は、教科書にも載っている用途です。その他、

・不等式の証明で、０以上になる式の形（２乗の和）を作るため

にも使われます。「相加相乗平均」の証明もそうですね。

平方完成という計算は、展開 それとも 因数分解 どっち？

そのような質問が出ました。
その答えは、どちらでもないのです。

中３で出てきた「乗法公式」が有名です。
あれは確かに、展開と因数分解の計算ですが、平方完成では、それらを移項など変形させた形で使っているので、展開とも因数分解とも違った方向性の、計算方法と言えます。